简化二极管电路的分析方法

由二极管组成的电路是非线性电路，它的分析方法有图解分析法和模型分析法。在工程中通常采用模型分析法。本节介绍几种常用的二极管模型，它是在特定的条件下，将非线性的二极管伏安特性分段线性化处理，从而可以用某些线性元件组成的电路（模型）来近似代替二极管，把非线性的二极管电路转化为线性电路来求解。

二极管的电路模型有下列几种：

（1）二极管的理想模型 在分析二极管应用电路时，当二极管的正向压降和正向电阻与外接电路的等效电压和等效电阻相比均可忽略时，可以把二极管看作是理想二极管，即二极管外加正向电压时，U_D=0V；二极管外加反向电压时，I_D=0A。它在电路中相当于一个理想开关。二极管理想的模型如图2-14所示。

（2）二极管的实用模型 根据二极管伏安特性的分析，在实际应用中，当二极管的正向压降与外加电压相比不能忽略，而正向电阻和外接电阻相比可忽略时，可以将二极管等效为二极管的实用模型。对于硅二极管来说，可以采用0.7模型，即加正向电压时，硅管的导通电压降U_D=0.7V；加反向电压时，反向电流很小，认为反向电流I_D≈0A。由此得到硅二极管的实用模型的伏安特性曲线如图2-15所示。锗二极管实际应用时则采用0.3模型，即正向导通时，锗管的导通压降U_D=0.3V；加反向电压时，认为反向电流I_D≈0A。

（3）小信号模型 以上两种模型，适用于研究较大范围的电流、电压关系，称为小信号模型。

如图2-16a所示，在二极管电路中，除直流电源外，如果再引入幅值很小的交流信号，则二极管两端的电压及通过它的电流将在某一固定值（直流量）附近做微小变化。

此时，可用二极管在该固定值处的动态（微变）电阻r_d来近似代替二极管，称为二极管的小信号模型（或微变模型），如图2-16b所示。微变电阻r_d通常由式（2-5）求解，即

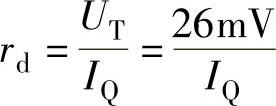
式中，I_Q为通过二极管的直流电流（A），可见I_Q不同时r_d不同。

例2-1 硅二极管电路如图2-17所示，试分别用二极管的理想模型、实用模型计算电路中的电流I_D和输出电压U_o。

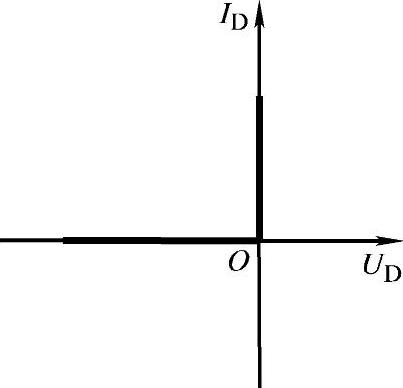
图2-14 二极管的理想模型

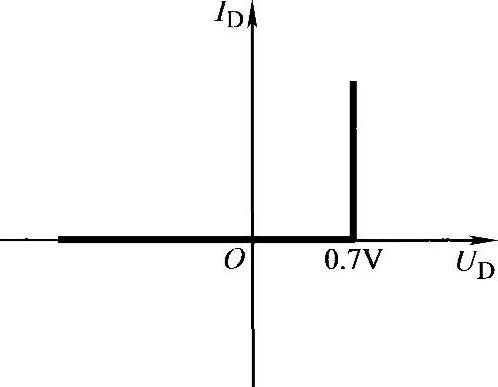
图2-15 硅二极管的实用模型

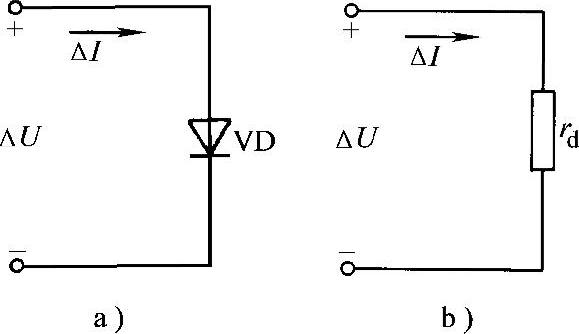
图2-16 二极管小信号模型

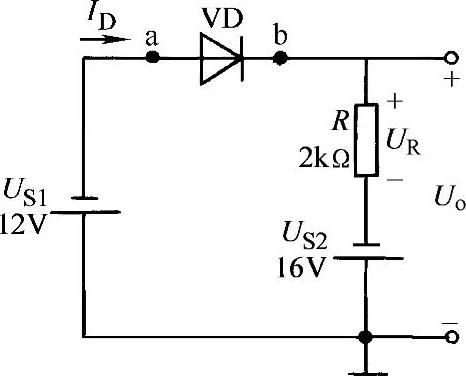
图2-17 例2-1的电路图

解 首先要判断二极管VD是导通还是截止。为此，可假定移去二极管VD，计算连接二极管两端处的电位U_a和U_b。由图2-17可知

U_a=-12V U_b=-16V(www.xing528.com)

因为U_a＞U_b，且U_a-U_b＞0.7V，故在理想模型和实用模型中，二极管VD均导通。

1）用理想模型。由于二极管VD导通，其管压降U_D=0V，所以

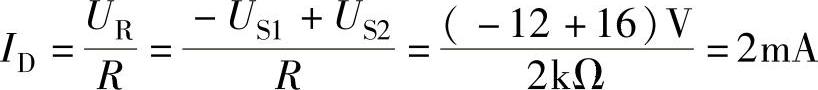
U_o=-U_S1=-12V

2）用实用模型。由于二极管VD导通，其管压降U_D=0.7V，所以

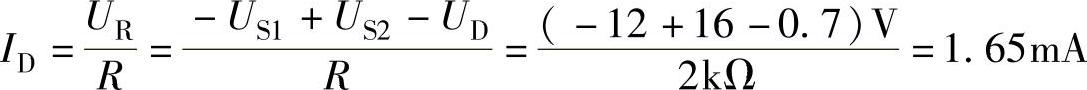
U_o=I_DR-U_S2=1.65mA×2kΩ-16V=-12.7V

例2-2 已知如图2-18a所示电路中，U_S1=6V，u_S2=0.2sinωtV，R_S=1kΩ，二极管为硅管，试求通过二极管的电流i_D。

解 首先令u_S2=0，利用二极管的实用模型，求出二极管的直流工作电流I_Q，如图2-18b所示，得

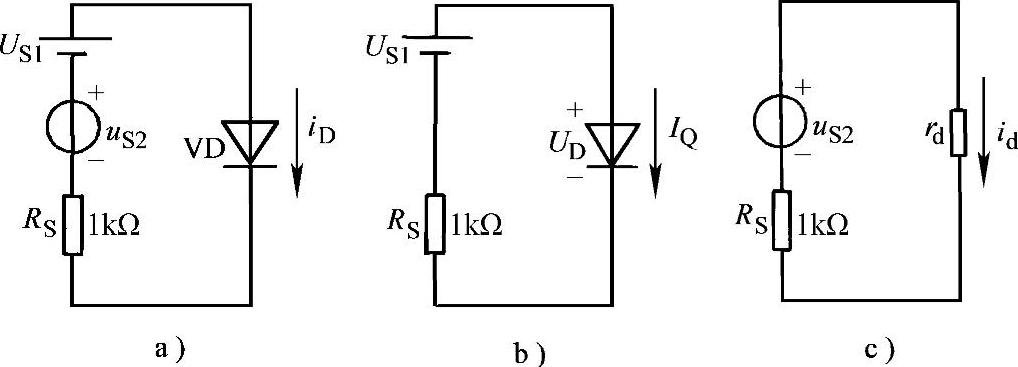
图2-18 例2-2的电路图

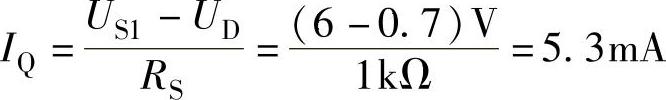
根据式（2-5）求出二极管的动态电阻

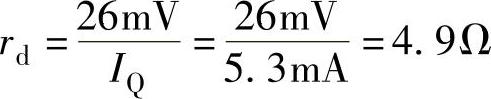
然后，令U_S1=0，利用二极管的微变模型，求出流过二极管的交流电流i_d，如图2-18c所示，有

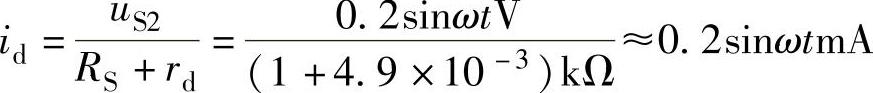
所以流过二极管的电流

i_D=I_Q+i_d=（5.3+0.2sinωt）mA

由此可见，模型分析法简单明了，它虽然存在一定的近似性，但只要模型选择合理，分析结果所带来的误差在工程上还是允许的。