以水作为集热工质的平板集热器(见图5.11)在热虹吸型太阳能热水器中非常普遍。为了计算流体出口温度,提出了集热器热转移因子的概念。这个因子反映稳态时吸热板(通常为翼管式结构)的传热特性,它是集热器流体实际得到的热量与假设集热器处于流体入口温度下得到的热量之比(见图5.11)。

图5.11 以水作为集热工质的平板集热器
热转移因子表示流体流过集热器某一点实际吸收的热量与假设整个翼板处于局部流体温度时所吸收的热量之比。因此,可以把集热管分成若干小段,假设每一段的热转移因子为常数。对每一段或每个节点的流体进行瞬态热分析,利用局部热转移因子计算吸热板与流体之间的传热量。此外,由于每一个节点的流体温度是已知的,当确定热虹吸系统中流体的质量流量时,无需假设进出口温度的线性分布,便可准确地计算出集热器中浮力对换热量的贡献大小。集热板与流体的最高温度间存在时间延迟,这部分是因为集热板的瞬时特性对集热器的出口温度会产生显著影响(Shitzer等,1979)。
在高质量流量下,平板集热器Hottel-Whillier-Bliss模型与稳态有限差分模型所预测的水温分布非常吻合(Kirchhoff和Billups,1976)。然而,在热虹吸的质量流量较低的情况下,Hottel-Whillier-Bliss模型预测的效率会过高。这是因为在低质量流量下,平板集热器上平行于排管方向的热流通量会显著增加,而Hottel-Whillier-Bliss模型分析中并未考虑到这点。
因此,为准确预测热虹吸系统中平板集热器的效率,需要建立二维瞬态有限差分模型。相比于Hottel-Whillier-Bliss模型,其优势在于:①对流体、集热板和玻璃盖板的热容量和温度曲线分别进行假设;②采用更少的假设来分析集热板内和集热板与流体之间的传热过程。然而,即使是在精细的集热器仿真模型中,也可以通过假设避免预测不随空间与时间变化的参数。对于含有翅片和平行管结构的集热板,通常包含以下假设:
1)为便于考虑辐射换热,玻璃盖板和集热板通常看作是两个大面积、相互平行的灰体。
2)玻璃盖板用一个单独的节点来表示,因此,在任一时刻玻璃盖板上各点的温度可认为是相同的。
3)玻璃盖板对长波辐射是不透明的。
4)由于翅片很薄,其温度梯度可视为常数,且仅考虑二维传热。
5)忽略集热器流体沿流动方向的导热。
二维吸热板温度分布的能量平衡如图5.12所示。
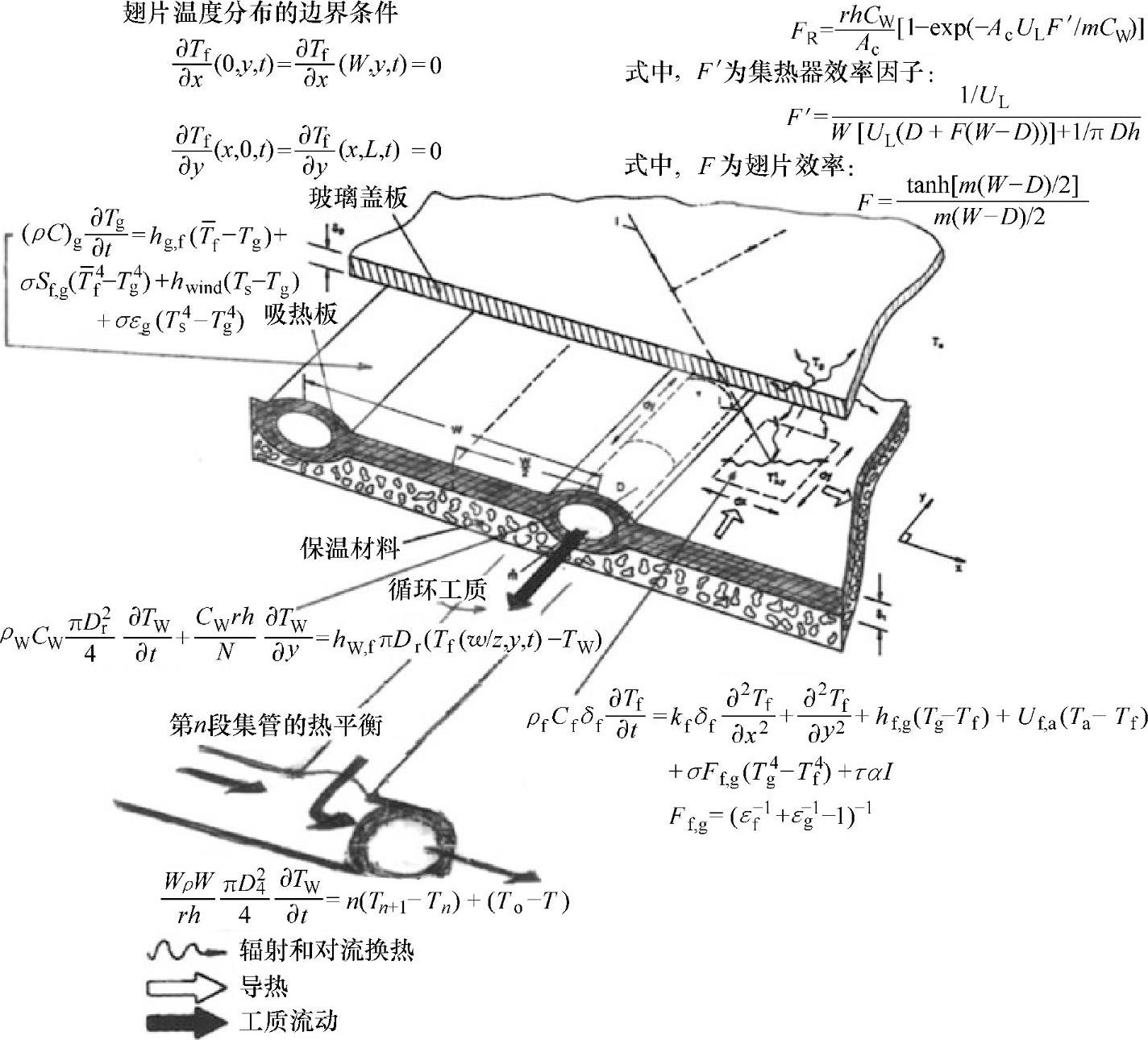
图5.12 太阳能集热器吸热板的能量平衡
根据排管内流体增量的热平衡,可以得到流体温度和集热板温度间的边界条件。假设管壁和集热板翅片的局部温度相同,集热板翅片与流体间的对流换热量等于内能增量与从下游方向进入流体增量的对流传热量之和。为了避免使用复杂的形状因子,通常假设玻璃盖板温度不随时间而变化,且盖板温度由能量平衡关系得出。玻璃盖板与集热板间的换热量由集热板的平均温度确定。玻璃盖板内能的增长率等于以下各项之和:①集热板与盖板间的对流换热量;②集热板与盖板间的辐射换热量;③玻璃盖板外部与环境间的对流换热量(主要为风效应);④玻璃盖板与天空的辐射换热量。
为了准确模拟集热器的瞬态响应时间,需要考虑集热器集管内水的热容量。流体在集管中的瞬态响应反映了实验中所观察到的时间延迟,即排管末端流体温度发生变化的时刻与该变化出现在集管出口时刻之间存在时间差。集管的质量流量受到各排管的影响,且每根排管所造成的影响各不相同。因此,有必要对每根排管及其翅片单独进行考虑,如图5.13所示。集管-排管型集热器排管中的流量分配可能是非均匀的(Jones和Lior,1978)。集热器的每根排管都会分别对出口温度产生不同的影响。

图5.13 吸热板管板结构的能量平衡
集热器吸收的热流量与其向外界环境散失的热流量之差为工质带走的热流量(当考虑集热器各部件储存或释放的热量时,对应的瞬态方程中会出现一个附加项)。对于一维模型中集热器的离散单元,有效热容为一定值,并忽略沿流体流动方向的导热。假设集热器在流体流动方向上具有同质性,所考虑单元的有效热容(MC)dx表达式如图5.13所示。
放热周期(Roger,1980)表示从集热器排出的工质所具有的热容量逐渐增加到集热器系统有效热容量的过程所需的时间。集热器系统的热输出率可用卷积积分表示(Kuo,1966),它说明了由集热器有效热容导致的出口温度延迟,如图5.13左侧区域所示。图5.13右侧区域括号内的第一部分是集热器的响应函数,第二部分表示在所考虑的一般工况下对工质的能量输入率。因此,集热器响应函数的表达式如图5.14所示。(https://www.xing528.com)
响应周期表示集热器的响应函数由初始值增加到0.368时所经过的时间。对应于一阶系统的响应周期的标准定义为:当相关变量的变化率恒为初始值时,完成瞬态过程所经过的时间段(Atkinson,1980)。在稳态工况下,集热器的响应函数成为单一值,即热迁移因子。

图5.14 太阳能集热器的响应函数
集热器瞬态运行下动态效应的理论分析已得到开展(DeRon,1980;Kamminga,1985;Chakraverty等,1987;Wang等,1987)。通过简化模型(例如,图5.14右上方所示的方程),可以对瞬态工况下集热器的长期性能进行很好的预测(Hill等,1977;Si- mon,1975;Gillet和Moon,1985)。它们已经被广泛用于推导太阳能集热器各种特性的表达式,例如响应周期(Hill等,1977)和有效热容量(Simon,1975)。然而,由于进行了简化假设,不能充分预测短期运行的性能,比如在间歇性太阳辐射条件下的逐时热性能。
假设有效热容为一单值且沿流体流动方向的热传导可以忽略,则当已知太阳辐射随时间的变化规律时,可以获得太阳辐射强度在一般性时间变化模式下的精确解析解。例如,考虑太阳辐射强度从零开始的阶跃变化。假定环境温度和入口温度相等,并且在瞬态阶段过程中保持不变。对于这种特殊情况,可获得如图5.15所示的解。此外,图5.15还显示了瞬态阶段温度分布的变化。
图5.15和图5.16表示了沿流体流动方向不同流段最早达到稳态温度的时间,这一时间由流段位置决定。最靠近集热器入口位置的流段最先达到稳态,然后稳态“前锋”逐步向集热器出口方向移动。在运行时间达到稳态分析得到的放热时间(Klein等,1974)后,这个“前锋”到达出口处。
在瞬态工况下,太阳能集热器的局部热性能是不均匀的。沿流体流动路径的不同位置处温度改变的响应模式不同,如图5.16所示。响应函数需要考虑集热器出口温度与时间和位置的相关性。但是,这样的响应函数无法轻易通过分析和实验得到。如果假设瞬态运行过程可以近似为一系列离散的阶跃变化,每段持续时间不小于集热器的放热时间,使得出口温度与集热系统分布特性的相关性可被认为是每个阶跃变化的平均效果。那么,集热器的热性能可以用一个单一变量响应函数来描述,该函数可以由出口温度值推导出,如图5.16中的实线所示。考虑到集热器分布特性的整体影响,图5.17给出的集热器响应函数呈现出近似方形的分布(与图5.14中的曲线相比),曲线的指数特性非常平缓。
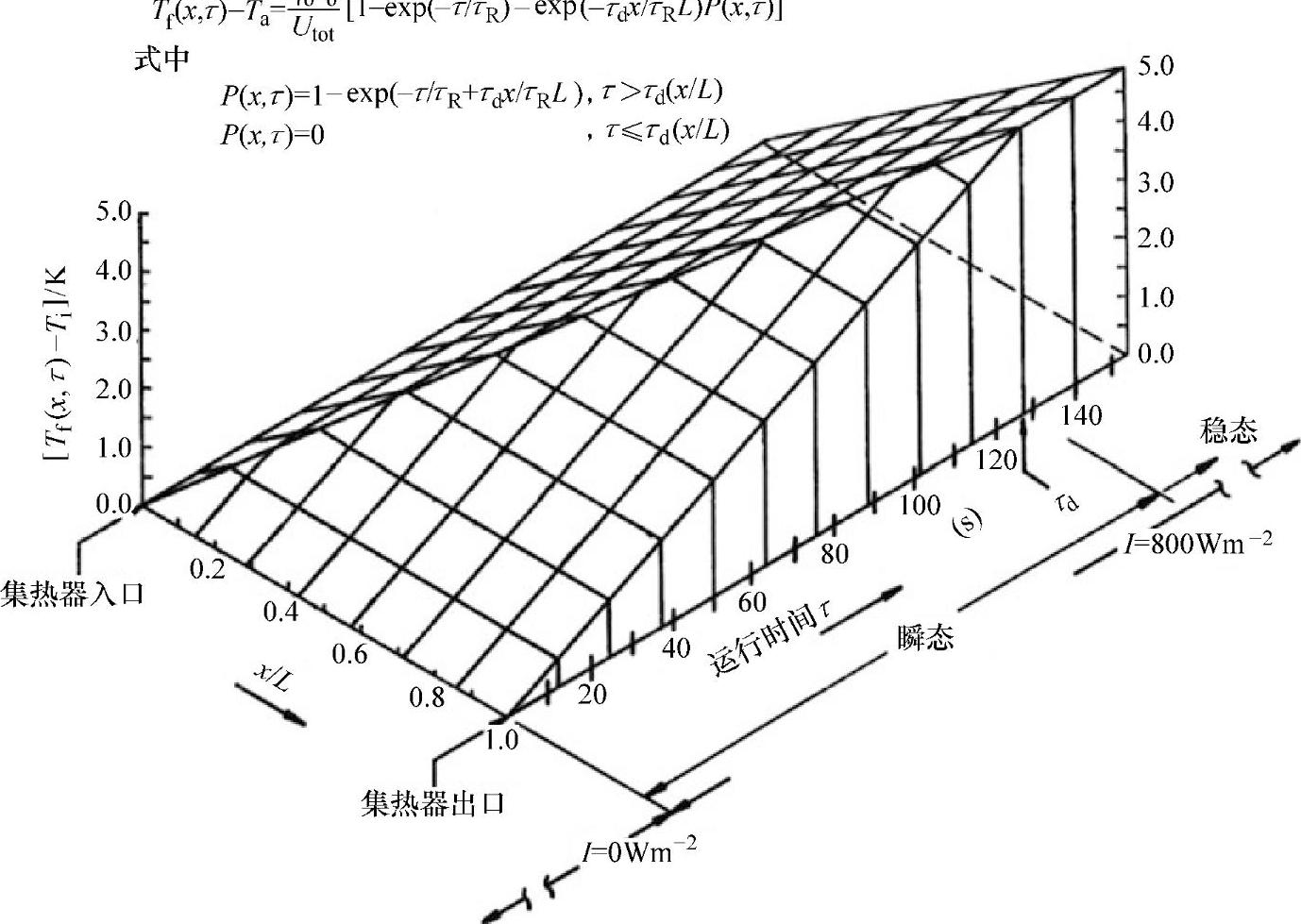
图5.15 集热板温度响应函数

图5.16 集热板瞬态热状态的变化

图5.17 太阳能集热器的响应函数和滞后因子
瞬态工况下有效热容的性能不能用单一数值来描述(Prapas等,1988a,b),它可以用图5.17的左上角所示的函数表示。
图5.17中的滞后因子对应于从瞬态阶段开始所用的运行时间。瞬态阶段的有效热容大于稳态工况下的值。在瞬态工况下,热量在传输到工质之前储存在集热板中。在稳态工况下,大多数金属吸热板可在10s内达到接近于渐近线的稳态热容值。
如果集热器采用有效的瞬态热容,热平衡方程则变为非线性。响应函数只能通过对该方程的线性化处理近似获得。然而,吸热板-工质子系统的响应周期约为0.4s,远小于典型金属吸热板集热器的放热时间130s。假设逐步瞬态变化的持续时间大于放热时间,从而使得热容响应能在瞬态间隔内平均化。所以,尽管从数学的角度无法获得一般的解析解,但利用简化实验可以获得集热器系统的“响应函数”。通过结合集热器分布特性和有效热容的平均效应,只要运行条件随时间间隔呈阶跃式变化且两个连续变化的时间间隔比放热时间长,后一个方程就可充分描述集热器系统的瞬态性能。这个实验获得的响应函数与基于恒定有效热容假设所导出的函数在形式上有所不同(见图5.17中的曲线1)。该函数的定性形状如图5.17中的曲线2所示。
如果假设图5.13中位置1和位置2之间的管道热容为0,则在位置2处测量的与出口温度相关的响应函数形式与图5.17所示的曲线3相同。对应于位置1相关的响应函数(即曲线2),可以根据管道尺寸和流体流量预测滞后时间。在典型的集管-排管式平板集热器吸热板的翼管结构中,当通过集热器排管的流量均匀分配时,集热器系统的整体响应函数可以由每根排管的响应函数线性叠加得到。图5.18定性地给出了总响应函数的曲线。总响应可被认为取决于集热器内管道的几何形状以及出口温度的测量位置。

图5.18 集热器整体响应函数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




