RLC串联电路分析及应用优化技巧

【任务目标】

•知识目标

(1)掌握RLC 串联电路中各元件电气量之间的关系;

(2)掌握RLC 串联电路的分析方法;

(3)掌握RLC 串联谐振含义与分析。

•能力目标

(1)能识读电路图;

(2)能正确按图接线;

(3)能使用电流表、电压表、万用表等进行电阻与电感参数的测量;

(4)能进行实验数据分析;

(5)能完成实验报告填写。

•态度目标

(1)能主动学习,在完成任务过程中发现问题、分析问题和解决问题;

(2)能与小组成员协商、交流配合完成本次学习任务,养成分工合作的团队意识;

(3)严格遵守安全规范,爱岗敬业、勤奋工作。

【任务描述】

班级学生自由组合为若干个实验小组,各实验小组自行选出组长,并明确各小组成员的角色。 在电工实验室中,各实验小组按照《Q/GDW 1799.1—2013 国家电网公司电力安全工作规程》、进网电工证相关标准的要求,进行RLC 串联电路各电气量的测量。

【任务准备】

课前预习相关知识部分,独立回答下列问题:

(1)RLC 串联电路中各元件电气量的关系?

(2)RLC 串联电路中的功率关系?

(3)RLC 串联谐振产生的条件?

【相关知识】

理论知识

一、 RLC 串联电路电流与电压的关系

图3.3.1　RLC 串联电路

RLC 串联电路如图3.3.1 所示。 对于串联电路而言,其所有元件的电流相同,即电阻、电感与电容的电流相同。 因此,可选择电流为参考相量,假设流经RLC 串联电路的电流为i =Im sin ωt,初相角为零。

设电阻、电感与电容的电压分别为uR、uL 与uC,则其对应的电压有效值分别为

通过画相量图的方法即可求出总电压,如图3.3.2 所示。 图3.3.3称为电压三角形,可反映出RLC 串联电路中各电压之间的关系。

图3.3.2　RLC 串联电路相量图

图3.3.3　电压三角形

由电压三角形可求得端电压的有效值,即

也可求得端电压与电流的相位差,为

在串联电路中,因电流相同,所以相量电压关系式又可写成

设Z=R+j(XL -XC),Z 称为此串联电路的复数阻抗,简称阻抗。 其中X =XL -XC,称为电抗。 感抗XL 和容抗XC 总是正的,电抗X 则是代数量,可正也可负。 可通过阻抗Z 将电路中的相量电压和相量电流联系起来。

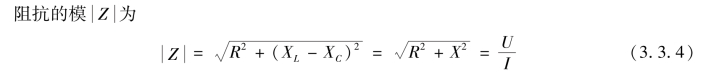
阻抗三角形的底角φ 称为阻抗角,也就是端电压与端电流的相位差,于是可得相位差与电路参数的关系。

阻抗的辐角φ(阻抗角)为:

图3.3.4　阻抗三角形

由上所述可见:

RLC 串联电路的端电压与电流有效值之比值等于阻抗构成阻抗三角形,它与电压三角形是相似三角形。 阻抗角φ 取决于电路的参数与电源的频率,它反映了端电压与电流的超前与滞后关系。

根据式(3.3.5),随着XL 和XC 的值不同,RLC 串联电路有三种情况。

(1)XL ＞XC。 此时φ ＞0,表明电压超前于电流。 图3.3.4(b)的相量图就是按这种情况画出的,这种电路称为电感性电路。

(2)XL ＜XC。 此时φ ＜0,表明电压滞后于电流。 其相量图如图3.3.5 所示,这种电路称为电容性电路。

(3)XL =XC。 此时φ=0,表明电压和电流同相位。 其相量图如图3.3.6 所示,这种电路称为电阻性电路。 由于电路在这种情况下发生谐振,有其特殊的一些现象,将在以后专门进行讨论。

图3.3.5　电容性电路的相量

图3.3.6　电阻性电路的相量

【例3.3.1】　已知RLC 串联电路的R=8 Ω、XL =10 Ω、XC =4 Ω,通过I=2 A 的正弦电流。 试完成:

(a)求电路端电压的有效值。

(b)以电流i 为参考正弦量,写出电路端电压u 的表达式。

(c)以端电压为参考正弦量,写出电流i 的表达式。

解　(a)电路的阻抗

端电压有效值

(b)以电流为参考正弦量,即设电流的初相为零,则

而阻抗角

φ ＞0,表明电路为电感性,即u 超前i 36.9°,故

(c)以端电压u 为参考正弦量,即设电压的初相为零,则

因u 超前i 36.9°,也就是i 滞后于u 36.9°,故i=Im sin(ωt-φ) =2 2 sin(ωt-36.9°)A。

【例3.3.2】　已知RLC 串联电路中,R 为4 Ω,XL 为9 Ω,XC 为6 Ω,电源电压U 为100 V,试求电路中的电压和电流的相位差及电阻、电感和电容上的电压。

解　已知U=100 V,XL =9 Ω,XC =6 Ω,R=4 Ω。 由此得出

电路的电抗X=XL -XC =9 -6 =3(Ω)

电阻上的电压为

电感上的电压为

电容上的电压为

答:相位差为36.87°,电阻、电感、电容上的电压分别为80 V、180 V 和120 V。

【例3.3.3】　在RLC 串联电路中,已知R =3 Ω,L =12.74 mH,C =398 μF,电源电压U=220 V, f=50 Hz,选定电源电压为参考正弦量。

(a)求电路中的电流相量及电压相量;(b)写出i、UR、UL、UC 的解析式。

解　(a)求电路中的电流相量及电压相量

设各电压和电流的参考方向均一致,故有

(b)根据电压、电流的相量式,写出对应的解析式为

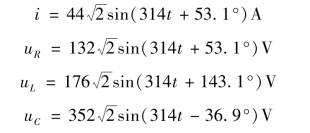
二、RLC 串联电路功率关系

图3.3.7(a)所示的RLC 串联电路,电压和电流取参考方向时,电路吸收的瞬时功率为

图3.3.7(b)画出了以电流为参考正弦量时pL 和pC 的波形,以及它们之和(pL +pC) 的波形。 因uL 与uC 反向,故pL 与pC 的符号总是相反的。

当pL 为正值时,电感吸收能量,而此时pC 为负值,电容放出能量;当pL 为负值时,电感放出能量,而此时pC 为正值,电容吸收能量。 因此,L 与C 之间正好进行能量交换,既相互补偿,补偿后的差值再与电源进行交换。

(pL +pC)的曲线与电阻元件R 的瞬时功率pR 的曲线相加,可得到整个电路的瞬时功率p 的曲线,如图3.3.7(c)所示。

瞬时功率的实用意义不大,但从曲线可以看出,一个周期内有两段时间p ＞0,此时电路从电源吸收能量,其中一部分供电阻消耗,另一部分转变成场能储存在储能元件中,其余两段时间p ＜0。 此时电路发出能量,这是因为储能元件放出场能,除一部分供电阻消耗外,其余送回电源。 由于p 曲线与时间轴所围的正面积大于负面积,所以电路的平均功率不为零。

图3.3.7　RLC 串联电路及瞬时功率的波形

1)有功功率

有功功率是指瞬时功率在一周期内的平均值。 由于pL 和pC 在一周期内的平均值为零,所以电路瞬时功率p 的平均值等于电阻元件瞬时功率pR 的平均值,即P=PR =URI。

根据RLC 串联电路的电压三角形,UR =Ucos φ,故

或

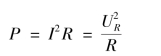
所以RLC 串联电路的有功功率就是电阻元件消耗的有功功率。

2)无功功率

无功功率是指储能元件与电源交换功率的最大值,由于电感元件和电容元件的瞬时功率在相互补偿,与电源交换的只是它们的差值,因此RLC 电路的无功功率为

或

单位为var(乏)。

QL 和QC 总为正值,Q 则可正可负。 当电路呈感性(XL ＞XC)时,电感元件的磁场储能与电容元件的电场储能交换外,多余的部分再与电源进行交换。 Q ＞0,表示其为电感性无功功率。 当电路呈容性(XL ＜XC)时,电容的电场储能除与电感元件的磁场储能交换外,多余部分再与电源交换。 Q ＜0,表示其为电容性无功功率。 无功功率只用来表明电路与电源交换功率的规模,而不代表消耗功率。 但在电力系统中,习惯将Q ＞0 称为电路消耗无功功率,而将Q ＜0 称为电路“发出”无功功率。

3)视在功率

电路的端电压和电流有效值的乘积称为视在功率,即(www.xing528.com)

或

单位为V·A(伏·安)。

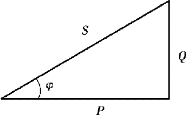
图3.3.8　功率三角形

P、Q、S 三者关系如图3.3.8 所示。 图中P 为有功功率,表示电阻元件消耗的电功率;Q 为无功功率,表示电感电容与电源交换功率的最大值;S 为视在功率,单位为伏安(V·A),表示电路的总功率。 通常,用电设备的额定电压与额定电流的乘积为额定视在功率。

根据功率三角形可得

即三者构成直角三角形关系,与RL 串联电路不同的是,RLC 串联电路的功率因数角可正可负。

4)功率因数

与RL 电路一样,RLC 串联电路的有功功率与视在功率的比值为功率因数,即

也可以写成

【例3.3.4】　一RLC 串联电路,R =40 Ω,XL =50 Ω,XC =80 Ω,通过I =2 A 的正弦电流,求电路的P、Q、S 和λ,并画出功率三角形。

解　先求电路的阻抗和阻抗角

电路端电压有效值

有功功率

无功功率

视在功率

功率因数

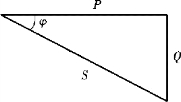
图3.3.9　【例3.3.4】图

功率三角形如图3.3.9 所示。

三、RLC 串联电路串联谐振

含有电感和电容的交流电路,在一般情况下,电路的端电压和电流是有相位差的。 但在一定条件下,端电压和电流可能出现同相位的现象,称电路发生谐振。 谐振在电信工程中有着广泛的应用,但在有些场合也可能造成某种危害,因此研究谐振有着重要的实用意义。

1)串联谐振的含义

频率会影响感抗与容抗的大小,因此,RLC 串联电路的端口电压与电流之间的相位差会随着频率的变化而变化。 对于RLC 串联电路而言,若其端口电压与电流同相位时,整个电路呈阻性,这种状态称为谐振,如图3.3.10 所示。

图3.3.10　RLC 串联谐振电路

由谐振的定义可知,RLC 串联电路发生谐振的条件为

由此可推出XL =XC。

谐振时的角频率

谐振频率

由上式可见,f0 取决于电路的参数L 和C,而与R 无关。 只要L 和C 一定,就有一个与之对应的谐振频率f0。 所以f0 反映了电路的一种固有的性质,也称为电路的固有频率。 只有当外加电压的频率f=f0 时,电路才发生谐振。

如果外加电压的频率一定,也可以通过改变L 或C 来使电路达到谐振。 收音机电路就是通过调节可变电容器来使电路达到谐振的。 调节谐振的过程称为调谐。

【例3.3.5】　一收音机的输入电路中,电感L=0.233 mH 与可调电容C=42.5 ～360 pF串联,求谐振的频率范围。

解　C=42.5 pF 时的谐振频率

C=360 pF 时的谐振频率

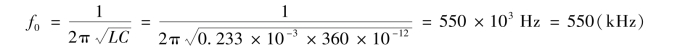
频率范围为550 ～1 600 kHz。

【例3.3.6】　某串联电路中R=10 Ω、L=64 μH、C=100 μF,电源电动势E =0.5 V,求发生谐振时各元件上的电压。

解

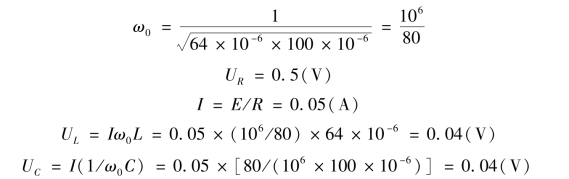
答:UR 为0.5 V,UL 为0.04 V,UC 为0.04 V。

2)串联谐振的特征

(1)电路的阻抗最小,同时电路电流最大。 阻抗可由下式求得

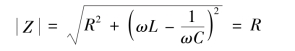
串联谐振电路中的电流为

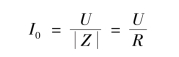
达到谐振时电流的最大值,称为谐振电流,实际电路中常以出现谐振电流I0 来判断是否发生谐振。

(2)电感电压和电容电压大小相等,方向相反。 发生谐振时的感抗和容抗称为特性阻抗,记为ρ,即

特性阻抗ρ 与电阻R 的比值,用品质因数Q 表示,工程上简称Q 值。

谐振时的电感电压和电容电压分别为

因此

实际上,Q 值一般可达几十至几百,因此,在发生串联谐振时,电感电压与电容电压可高出外加电压几十倍以上。 在电信电路中,可将微弱的电信号输入串联谐振电路中,通过谐振,可从电容两端提取比输入高Q 倍的电压信号。 在电力电路中,需要避免谐振现象发生,否则电感与电容两端过高的电压可能将电气设备的绝缘击穿。

串联谐振也称为电压谐振。 谐振时的电感电压和电容电压大小相等,但相位相反,因而电感电压相量和电容电压相量相互抵消,外加电压全部作用于电阻两端,即

(3)谐振时,电路与电源之间不发生能量交换,能量交换只在电感和电容之间进行。

3)串联谐振的频率特性

频率特性是指电路的感抗、容抗和阻抗随频率变化的特性。

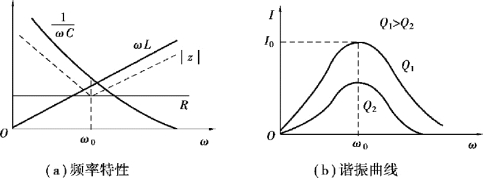
图3.3.11　频率特性

由可画出各量随ω(或f)的变化曲线,如图3.3.11(a)所示。谐振曲线即电流I 随频率ω(或f)的变化曲线,可由作出,如图3.3.11(b)所示。在ω=ω0 时,称为谐振电流。 当电源电压U 一定时,是定值,R 越小,I0 越大,谐振曲线就越尖锐。 电源角频率ω 与电路的谐振角频率(即固有振荡角频率)ω0 相差越大,则电流减小得越多。 当多个幅值相同而频率不同的电源(信号)同时作用于RLC 串联电路时,角频率与ω0 相同的电流为最大(即达谐振电流),偏离ω0 越远的电流将越小。 这表明RLC 串联电路对非谐振频率的信号具有较强的抑制作用,而对谐振频率的信号则使之显著突出,这种性质称为“选择性”。 谐振曲线尖锐与否,和R 有关,也就是和Q 值有关。 R 越小,Q 值越大,谐振曲线就越尖锐,选择性也就越好。 所以Q 值是反映串联谐振电路性质的一个重要指标,Q 值称为品质因数,原因也在于此。

实践知识

【任务简介】

1)任务描述

(1)验证RLC 串联电路中总电压和各元件电压的关系,总阻抗和各元件阻抗的关系,总功率和各元件的功率之间的关系。

(2)了解RLC 串联电路的三种性质。

(3)加深对串联谐振特点的理解。

2)任务要求

按照操作步骤完成RLC 串联电路电流电压与功率的测量,观察串联谐振的现象。

3)实施条件

表3.3.1　线圈参数的测定

【任务实施】

1)实验原理

RLC 串连电路中,根据元件参数L、C 及电源频率f 的大小不同,有以下三种情况:

(1)当电路的XL ＞XC 时,得UL ＞UC,阻抗角φ ＞0,则电压U 比电流I 超前,这时的电路称为感性电路。

(2)当电路的XL ＜XC 时,得UL ＜UC,阻抗角φ ＜0,则电压U 比电流I 滞后,这时的电路称为容性电路。

(3)当电路的XL =XC 时,得UL =UC,阻抗角φ=0,则为串连谐振电路,这时的电流I0 =U/(R+r)为最大,cos φ=1。

2)操作步骤

(1)按图3.3.12 接线。

(2)经检查后,合上电源开关K,调整调压器,使输出电压至100 V,并保持不变。

调整电容箱的电容,使其XL ＞XC(特点是UL ＞UC),C 调至24 μF 左右,此时cos φ 指针指在滞后0.95 左右的位置,即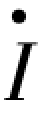滞后记录各元件的电流、电压和总电压、各元件消耗的功率和总功率于表3.3.2 中。

图3.3.12　RLC 串联电路实验电路图

调整电容量,使其XL ＜XC(特点是UL ＜UC),C 调至12 μF 左右,此时cos φ 指针指在超前0.8 左右的位置,即超前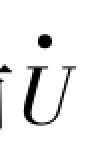,记录各元件的电流、电压和总电压、各元件消耗的功率和总功率于表3.3.2 中。

调整电容量,使其XL =XC(特点是UL =UC),C 调至19 μF 左右,此时cos φ 指针指在1的位置,即同相,记录各元件的电流、电压和总电压、各元件消耗的功率和总功率于表3.3.2 中,并观察谐振现象。

3)数据记录

表3.3.2　数据记录表

4)注意事项

(1)实验时应先测电压,后测功率,如发现元件电压超过瓦特表电压线圈的额定电压时,应更换量程。

(2)注意瓦特表和功率因数表使用方法和读数。

(3)实验接线前将调压器放在零位。

5)思考题

(1)仔细推敲实验电路中的接线,特别是功率表和功率因数表的接线及使用。

(2)根据测量数据计算各元件和全电路的参数。

(3)通过实验画出RLC 电路中三种情况下的相量图。

(4)分析串联谐振电路的特点及作用。

6)检查及评价

表3.3.3　检查与评价