RL串联电路在日光灯电路中的应用探析

【任务目标】

•知识目标

(1)掌握电阻、电感与电容元件在正弦交流电路中的基本特性;

(2)掌握RL 串联电路的分析方法。

•能力目标

(1)能识读电路图;

(2)能正确按图接线;

(3)能使用电流表、电压表、万用表等进行电阻与电感参数的测量;

(4)能进行实验数据分析;

(5)能完成实验报告填写。

•态度目标

(1)能主动学习,在完成任务过程中发现问题、分析问题和解决问题;

(2)能与小组成员协商、交流配合完成本次学习任务,养成分工合作的团队意识;

(3)严格遵守安全规范,爱岗敬业、勤奋工作。

【任务描述】

班级学生自由组合为若干个实验小组,各实验小组自行选出组长,并明确各小组成员的角色。 在电工实验室中,各实验小组按照《Q/GDW 1799.1—2013 国家电网公司电力安全工作规程》、进网电工证相关标准的要求,进行电阻与电感参数的测量。

【任务准备】

课前预习相关知识部分,独立回答下列问题:

(1)电阻、电感与电容元件在正弦交流电路中的特性如何?

(2)瞬时功率与平均功率是什么?

(3)RL 串联电路中的电压电流关系是怎样的?

(4)RL 串联电路中的功率关系。

【相关知识】

理论知识

电路中包含三种基本元件,分别为电阻、电感与电容。 因电阻、电感与电容本身的物理特性不同,有必要分析其在交流电路中的特点。

一、正弦电路中的电阻元件

电阻R 两端有正弦电压u= 2 U sin ωt V,则电阻中将有电流产生。 根据欧姆定律可知,在图3.2.1(a)中电压电流都为正方向的情况下,电流i 为

电阻元件的电压和电流的最大值(或有效值)之间都服从欧姆定律;在相位上,电压与电流同相,如图3.2.1(c)所示。

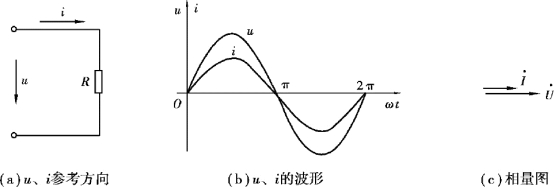
图3.2.1　正弦电路中的电阻元件

电流和电压写成相量的形式,为

所以

式(3.2.1)是电阻元件电压、电流关系的相量形式,它既表明了电流和电压的大小关系,又表明了它们同相的关系。

【例3.2.1】　已知电阻元件R=3 Ω,通过正弦电流=2∠30°A。 求关联参考方向下的电压,并画出相量图和波形图。

解　根据式(3.2.1)

电流和电压的相量图和波形图如图3.2.2 所示。

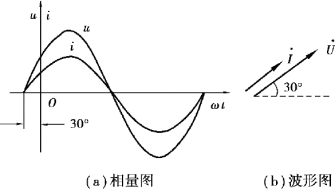
图3.2.2　【例3.2.1】图

瞬时功率p 为某单一元件瞬时电压与瞬时电流的乘积,即

对于电阻元件而言,其瞬时功率始终大于零,表示电阻元件始终吸收功率,将吸收的电能转换为热能。

因正弦交流电会随时间变化,元件的瞬时功率也随时间变化。 现引入平均功率,即元件瞬时功率在一个周期内的平均值,称为平均功率,并以P 表示。

当元件为电阻时,可求得其平均功率为

由欧姆定律可知,电阻元件的平均功率为

【例3.2.2】　一只220 V、100 W 的灯泡,接到u=311 sin ωt V 的电源上,求通过灯泡电流的有效值。

解

【例3.2.3】　有一额定电压UN =220 V、额定功率PN =1 000 W 的电炉,若加在电炉上的电压为u =200 2 sin(314t+π/4)V,试求通过电炉丝的电流i 和电炉的平均功率P。

解

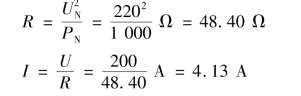
设电流i 与电压u 取关联参考方向,则有

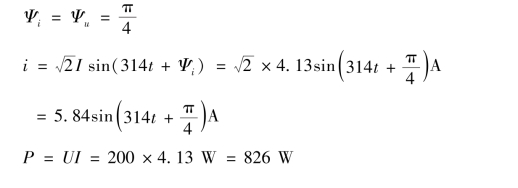
二、正弦电路中的电感元件

当正弦电流加入电感元件时,根据电磁感应定律电感元件内将产生感应电动势,电感元件两端具有电压。 当选取关联参考方向时,如图3.2.3(a)所示,可求得电感元件两端电压为

设通过电感的电流为i=Im sin ωt A,则可得电感两端电压为

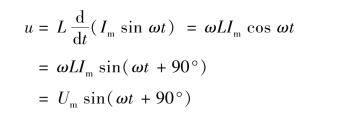
由此可得电感元件电压与电流的大小关系为

Um = ωLIm

电感元件电压与电流的相位关系为电压超前电流90°,如图3.2.3(b)(c)所示。

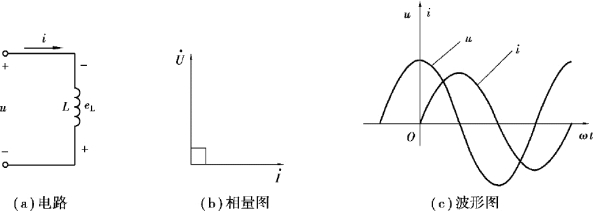
图3.2.3　电感元件

为方便表示电感元件电压与电流的关系,现引入新概念——感抗,即电感元件电压与电流幅值(有效值)之比,用XL 表示,单位为欧姆(Ω):

要注意,感抗只是电压与电流的最大值或有效值之比,而不是瞬时值之比,即

若将电流和电压写成相量的形式,并设电流为参考相量,则

所以

当电感电流的初相位为ψi 时,电感电压的初相ψu =ψi +90°,电压与电流之间的相位差φ=ψu -ψi =90°。

电感元件在交流电路中具有限流作用,它的限流、降压作用不仅与元件的电感量L 的大小有关,还与电感元件工作时的电流频率f 有关,频率越高,感抗越大,电感的限流能力就越强。 在直流电路中,频率f=0,所以感抗为0,电感元件在直流电路中做短路处理。

【例3.2.4】　一个L=100 mH 的电感元件,接于U=220 V 的正弦电源上,求下列两种电源频率下的感抗和电流。

(a)工频。 (b)f=5 000 Hz。解　(a)工频时的感抗

XL = ωL = 314 ×100 ×10-3 Ω = 31.4 Ω

电感元件中的电流有效值

(b)f=5 000 Hz 时的感抗

电感元件中的电流有效值

【例3.2.5】　一电感元件的L=127 mH,外加电压u =220 2 sin(314t +30°)V,求关联参考方向下的电流i。

解　感抗为

电流有效值

电流瞬时值表示式

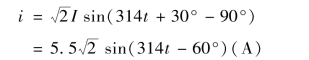
由瞬时功率的定义可知,电感元件的瞬时功率为

由上式可知,对于电感元件而言,其瞬时功率的频率为电流与电压的2 倍,即电流电压变换一个周期,瞬时功率变换两个周期,其波形图如图3.2.4 所示。

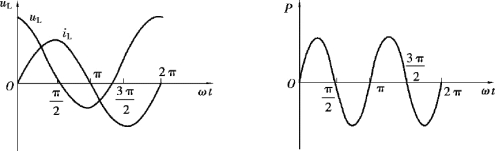
图3.2.4　电感元件的功率

由平均功率的定义可知电感元件的平均功率为

上式表明电感元件的有功功率为0,即在一个周期内消耗的电能为0。 电感元件的这个特点使得其在交流电路中被广泛应用,如使用电感元件来限制电路中的电流,交流电动机使用的启动电抗器等都应用到了电感线圈。

电感元件在交流电路中没有能量消耗,只与电源进行能量交换,交换过程中,电感的瞬时功率所能达到的最大值称为电感的无功功率QL。 电感元件瞬时功率的最大值为UI ,所以无功功率为

习惯上将电感元件的无功功率定为正值。

无功功率QL 不是电感元件做功的功率,它仅反映了电感元件与电源(或电感元件以外的电路) 进行能量交换的规模。 因此无功功率的单位为var(乏)或kvar(千乏)。

【例3.2.6】　已知电感元件的电感L=0.1 H,外加电压u=220 2 sin(314t+30°)V,试求通过电感元件的电流i 及电感元件的无功功率QL。

解

三、正弦电路中的电容元件

电容器是电路中的重要元件之一,用途非常广泛。 在直流电路稳定状态下,含电容器的支路相当于断路,但在交流电路中,电容器极板上的电荷将随着作用在极板上的电压变化而增减,因此使得与电容器极板相连的导线中出现交变电流i,如图3.2.5 所示。

在关联参考方向下,电容电压与电流之间的关系为

设电容两端电压为u=Um sin ωt V,则电容电流

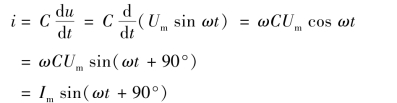
由此可知,电容两端电压与电流之间的数值关系为

Im = ωCUm

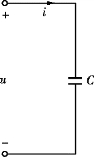
图3.2.5　电容元件

电容两端电压与电流之间的相位关系为电流超前电压90°。

为方便表示电容两端电压与电流之间的关系,现引入容抗概念。 容抗定义为电容元件两端电压与电流的幅值(或有效值)之比,用符号XC 表示,单位为欧姆(Ω):

要注意,容抗只是电压与电流的最大值或有效值之比,而不是瞬时值之比,即

用相量形式表示电容两端电压与电流之间的关系为

当电容电压的初相为Ψu 时,电容电流的初相Ψi =Ψu +90°,电压与电流之间的相位差φ=Ψu -Ψi = -90°。

电容在交流电路中也具有限流作用,限流作用的大小与电容量C 成反比,与频率f 成反比。 因为电容越大,电容存储的电荷量就越多,当电容有相同的电压变化时,电容越大,释放(或吸收) 的电荷就越多,因此电路中的电流就越大。 当频率f=0 时,即直流情况下,电容的容抗为无穷大,相当于开路。 也就是说,直流电流不能通过电容元件,电容元件具有“隔直”作用。

【例3.2.7】　一个C =100 μF 的电容元件,接于的电源上。 求:

(a)容抗。

(b)关联方向下的电流i。

(c)画出电压、电流的相量图。

解　(a)容抗

图3.2.6　【例3.2.7】图

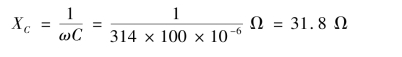
(b)电流有效值

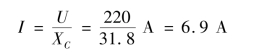
电流瞬时值表示式

(c)相量图如图3.2.6 所示。 电压和电流写成相量的形式,为

所以

(www.xing528.com)

电容元件的瞬时功率为

可以看出,对于电容元件而言,其瞬时功率的频率为电流与电压的2 倍,即电流电压变换一个周期,瞬时功率变换两个周期,其波形图如图3.2.7 所示。

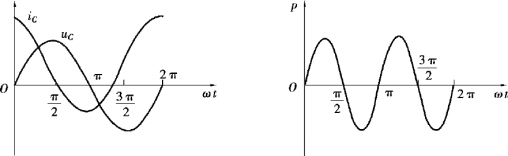
图3.2.7　电容元件波形图

电容元件的平均功率为

上式表明,电容元件的有功功率为0。 即对于理想电容元件而言,没有能量损耗,因此吸收的电能必然和放出的能量相等,一个周期内平均功率应等于零。

电容元件与外部电路进行能量交换时,瞬时功率的最大值称为电容的无功功率QC,有

通常以电流为参考得出的电感元件的无功功率QL 定为正值,电容的无功功率QC 为负值。

【例3.2.8】　求【例3.2.7】中电容元件的无功功率。

解　根据式(3.2.12)

【例3.2.9】　已知电容元件的电容C =100 μF,电容元件上的电压u = 20 sin(103t +60°)V,试求电容元件的电流i 和电容元件的无功功率QC。

解

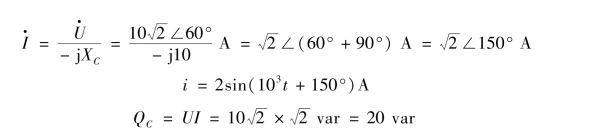
四、RL 串联电路分析

图3.2.8 为RL 串联电路。 在RL 串联电路中,设电阻为R,感抗为XL。 因电流相同,所以相量电压关系式又可写成

设Z=R+jXL,Z 称为此串联电路的复数阻抗,简称阻抗。 可通过阻抗Z 将电路中的相量电压和相量电流联系起来。

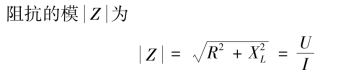
图3.2.8　RL 串联电路

阻抗的辐角φ 为(阻抗角):

1)瞬时功率

图3.2.8 所示的RL 串联电路,在关联参考方向下,吸收的瞬时功率为

RL 串联电路的瞬时功率等于电阻元件的瞬时功率和电感元件的瞬时功率之和。

2)有功功率(平均功率)

电路的有功功率是瞬时值p 在一周期内的平均值,用大写字母P 表示。 因为p =pR +pL,所以p 的平均值等于pR 的平均值和pL 的平均值之和。 由于后者为零,因此电路的有功功率P 等于pR 的平均值PR。

根据RL 串联电路的电压三角形,UR =U cos φ,故

式(3.2.13)是RL 串联电路的有功功率计算式。 它与直流功率的计算式P =UI 不同。它等于U 与I 的乘积,再乘以一个系数cos φ。 其中,φ 是电路的阻抗角,也是电压与电流的相位差。

3)无功功率

RL 串联电路只有电感元件是储能元件,所以电路的无功功率Q 就是电感元件的无功功率QL,它等于电感电压UL 与电流I 的乘积,即

无功功率的大小反映了电路与电源交换功率的规模。

4)视在功率

电路端电压和电流有效值的乘积称为视在功率,用大写字母S 表示,即

其单位为V·A(伏·安),较大的单位为kV·A(千伏·安)和MV·A(兆伏·安)。

有功功率P、无功功率Q、视在功率S 三者之间有以下关系

显然P、Q、S 构成一个直角三角形,如图3.2.9 所示。 阻抗三角形、电压三角形和功率三角形是3 个相似三角形,它们的大小依次递增I 倍。

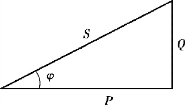
图3.2.9　功率三角形

5)功率因数

有功功率与视在功率的比值称为功率因数,用小写希腊字母λ 表示,则

式中φ 称为功率因数角,它是电压与电流的相位差,也是电路的阻抗角。

当视在功率一定时,功率因数越高,电路消耗的有功功率越大。

【例3.2.10】　已知一个RL 串联电路,其电阻和感抗均为10 Ω,在线路上加100 V 交流电压时,电流是多少? 电流电压的相位差多大?解　电路的阻抗为

电路中的电流为

电流电压的相位差为

答:电流为7.1 A,相位差45°。

【例3.2.11】　把一块电磁铁接到220 V,50 Hz 的电源上,只有当电流达15 A 以上时才能吸住电磁铁。 已知线圈的电阻XL =8 Ω,求线圈电阻不能大于何值。

解

答:R 小于12.3 Ω 时才符合要求。

【例3.2.12】　一个线圈接到220 V 的直流电源上时,其功率为1.21 kW,接到50 Hz,220 V 的交流电源上时,其功率为0.64 kW,求线圈的电阻和电感。

解

答:电阻为40 Ω,电感为0.38 H。

【例3.2.13】　一个RL 串联电路,R =30 Ω,L =127 mH,通过I =2 A 的工频正弦电流,求电路的P、Q、S 和λ。

解　先求感抗和阻抗

阻抗角

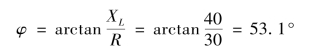
电路端电压有效值

有功功率

无功功率

视在功率

功率因数

【例3.2.14】　一电感线圈,通过工频正弦电流I=1 A 时,测得端电压U=20 V,有功功率P=12 W,求此线圈的参数R 和L。解　线圈的阻抗

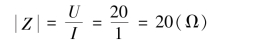
线圈的电阻

线圈感抗和电感

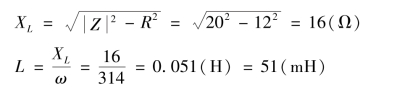
【例3.2.15】　日光灯导通后,镇流器与灯管串联。 镇流器可用电感元件为其模型,灯管可用电阻元件为其模型。 一个日光灯电路的R =300 Ω 、L =1.66 H,工频电源的电压为220 V,试求:电源电压与灯管电流的相位差、灯管电流、灯管电压、镇流器电压。

解　这是RL 串联电路,镇流器的感抗

电路的复阻抗

所以电源电压比灯管电流超前60.01°。

灯管电流

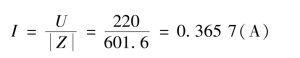
灯管电压、镇流器电压各为

实践知识

日光灯电路由灯管、镇流器和启辉器三个主要部分组成,由于镇流器的存在,日光灯电路为电感、电阻性电路,故使用电阻与电感串联电路来模拟日光灯电路。

【任务简介】

1)任务描述

(1)学会单相调压器和单相瓦特表的使用方法。

图3.2.10　实验模拟电路图

(2)掌握交流电流表、交流电压表和瓦特表,测量线圈参数(r 及L 值)的方法。

(3)通过本实验为在实际工作中从事输电、变电检修等方面打下良好的基础。

2)任务要求

测量线圈的阻值与电感。

3)实施条件

表3.2.1　线圈参数的测定

【任务实施】

1)操作过程

(1)用电流表、电压表和瓦特表三表法测量线圈参数按图3.2.11 接线,单相调压器放在零位,经老师检查后,合上开关K,逐渐将调压器的电压从0 升到50 V,记录电流表、电压表、瓦特表的读数于表3.2.2 中。

图3.2.11　实验接线电路图

(2)用三电压表法测线圈参数。 按图3.2.11 接线,经检查合上K,逐渐将调压器的电压从0 升到50 V,测量总的电压U,R 上的压降UR 及空心线圈UL 的压降并记入表3.2.3中。

2)数据记录

表3.2.2　数据记录表

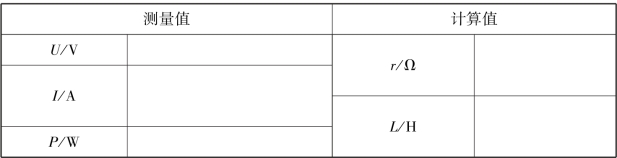
表3.2.3　数据记录表

3)注意事项

(1)注意单相调压器的输入端/输出端不能接错,否则会造成短路。

(2)合电源开关前必须检查单相调压器是否在零位。

(3)试验电压要按实验指导书上规定的值不能超过,否则会损坏线圈。

4)思考题

(1)将两种接线方式所测得线圈的参数与线圈的值比较,分析两种接线方式的适用范围。

(2)如何用实验方法判别负载是感性还是容性?

(3)用三表法测得的数据,计算出线圈的参数r 及L。

(4)用三电压表法测得的参数求出r、L,并与第一种方法进行比较。

5)检查及评价

表3.2.4　检查与评价

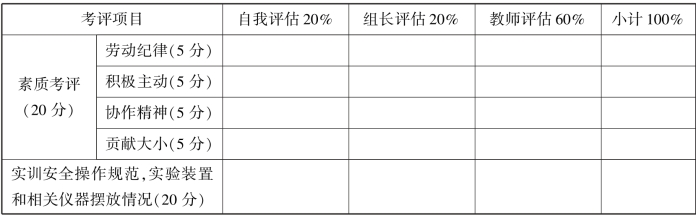
续表