单相交流电在白炽灯照明电路中的使用

【任务目标】

•知识目标

(1)掌握正弦交流电的特征量;

(2)掌握正弦交流电的表示方法;

(3)掌握正弦交流电的计算方法。

•能力目标

(1)能识读电路图;

(2)能正确按图接线;

(3)能使用电流表、电压表、万用表等进行交流电流、电压的测量;

(4)能进行实验数据分析;

(5)能完成实验报告填写。

•态度目标

(1)能主动学习,在完成任务过程中发现问题、分析问题和解决问题;

(2)能与小组成员协商、交流配合完成本次学习任务,养成分工合作的团队意识;

(3)严格遵守安全规范,爱岗敬业、勤奋工作。

【任务描述】

班级学生自由组合为若干个实验小组,各实验小组自行选出组长,并明确各小组成员的角色。 在电工实验室中,各实验小组按照《Q/GDW 1799.1—2013 国家电网公司电力安全工作规程》、进网电工证相关标准的要求,进行交流电流电压的测量。

【任务准备】

课前预习相关知识部分,独立回答下列问题:

(1)什么是交流电?

(2)正弦交流电的三要素是什么?

(3)如何用相量来表示正弦量交流电?

(4)如何进行正弦量的加减运算?

【相关知识】

理论知识

大小和方向都随时间变化的电流称为交流电流。 电工和电子电路中广泛应用交流电压源和电流源,其中按正弦规律变化的交流电源和信号,应用得也最为广泛。 交流电被广泛采用的主要原因:一是交流电压易于升高和降低,这样便于高压输送和低压使用;二是交流电动机比直流电动机性能优越,使用方便。 因此,发电厂发的电都是交流电,即使在需要直流的地方,往往也是将交流电通过整流设备变换为直流电。

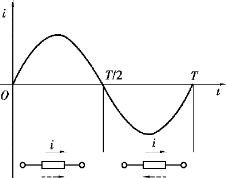
图3.1.1　正弦交流电流

正弦交流电的特点是它的大小随时间按正弦规律变化,如图3.1.1 所示。

正弦交流电变化一次所需的时间T 称为周期,单位为(秒,s)。 一秒钟内变化的次数称为频率f,单位是(赫兹,Hz)。 周期和频率的关系是

周期和频率都是用来表示交流电变化快慢的物理量。我国和大多数国家规定的电力标准频率为50 Hz,习惯上称此频率为工业频率,简称工频。美国和日本有的地区则规定60 Hz 为电力标准频率。

【例3.1.1】　求工频的周期。

解　根据式(3.1.1),周期为

交流电路中作用的电源或信号随时间不断地交变,因此,电路中各元件的电压、电流都是时间的函数。 为了确定出电路中各处电压、电流在任一瞬间的实际方向,因此在对电路进行分析之前,要对各电压、电流预先设定一个正方向,在电路中用“ +”“ -”号或箭头标出。

一、正弦量的特征量

1)正弦量的三要素

图3.1.1 所示的电流随时间变化的图形为电流的波形图,波形图的横轴为时间,纵轴高度表示出不同时刻下电流的数值。

图3.1.1 所示的波形图也可以用数学式描述,数学表示式为

式(3.1.2)为电流波形的瞬时表达式,其中Im 为电流的幅值,ω 为角频率,Ψ 为初相位。一个正弦电流(或电压) 量可以由上述三个特征量确定出来,这三个特征量称为正弦量的三要素。

(1)最大值(幅值)Im:反映正弦量变化的最高幅度(或称峰值)。

(2)角频率ω:反映正弦量变化的快慢,角频率ω 与频率f 之间有如下关系

它的单位是rad/s(弧度/秒)。

角速度ω 与频率f 只差一个常数2π,所以常将ω 称为角频率。 ω 与T、 f 一样,都反映正弦量变化的快慢。 直流电的大小和方向都不随时间变化,可以看成ω =0(即f =0 或T =∞)的一种特殊正弦交流电。

【例3.1.2】　已知电流i=311 sin(100πt),试求该电流的周期T 和频率。

解

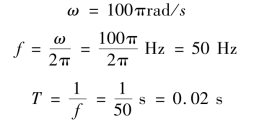
【例3.1.3】　已知正弦交流电的频率f=50 Hz,求其角频率ω。

解　ω=2πf=2π×50 =100π=314(rad/s)

(3)初相位Ψ。 (ωt+Ψ)是随时间变化的电角度,它决定了正弦量变化的进程,是正弦量随时间变化的核心部分,称为正弦量的相位或相角。 t =0 时的相位为Ψ,称为初相位,简称初相。 初相Ψ 的单位与ωt 一样为rad,但工程上习惯以(°)为单位,在计算时需将ωt 与Ψ变换成相同的单位。

【例3.1.4】　正弦交流电流的最大值Im =10 A,频率f=50 Hz,初相位Ψ=30°。 求

(a)t=0 时电流i 的瞬时值;

(b)t=10 ms 时电流i 的瞬时值。

解　(a)t=0 时,i=Im sin Ψ=10 sin 30° =5(A)

(b)t=10 ms,ωt=2πft=2π×50 ×10 ×10 -3 =π=180°

ωt+Ψ=π+30° =180° +30° =210°

所以i=Im sin(ωt+Ψ) =10 sin 210° = -5(A)

初相Ψ 的大小与计时起点的选择有关。 计时起点选得不同,初相就不同。 初相可以为正值,也可以为负值,但对其绝对值规定不超过180°,即

一个正弦电量,知道了它的最大值、频率(或角频率)和初相位后,该正弦电量随时间变化的规律就可以由数学表示式i=Im sin(ωt+Ψi)或u=Um sin(ωt+Ψu)来表示。

2)相位差

频率相同的两个或多个正弦电量,如果初相位不同,它们的相位角(ωt+Ψ)则不同。 两个同频正弦量的相位之差称为相位差,用φ 表示。

假设有两个同频率的正弦量e1 =Em sin(ωt+Ψ1)与e2 =Em sin(ωt+Ψ2),它们之间的相位差为

两个频率相同的正弦量的相位差有下述三种情况,以e1 =Em sin(ωt +Ψ1)与e2 =Em sin(ωt+Ψ2)两个同频率正弦量为例:

(1)0 ＜Ψ1 -Ψ2 ＜180°,这种情况称为e1超前e2,或e2滞后e1。 即e1的最大值比e2 的最大值先出现,如图3.1.2 所示。

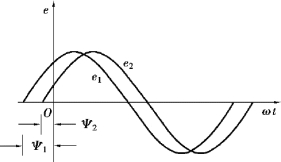
图3.1.2　同频率正弦量的相位差

(2)Ψ1 -Ψ2 =0,这种情况称为同相,即两个正弦量同增、同减,变化一致,如图3.1.3(a) 所示。

(3)Ψ1 -Ψ2 = ±180°,这种情况称为反相,如图3.1.3(b)所示。

相位差可用来描述正弦量之间的相位间关系。当多个同频正弦量同存于一个电路时,可以任选其中一个正弦量作为参考正弦量,令这个正弦量的初相位为零,则在这一电路中其他正弦量的初相位可由与参考正弦量的相位差来确定。

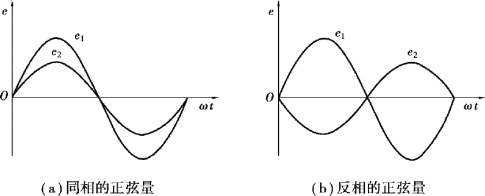
图3.1.3　正弦量的同相和反相

讨论相位差问题时应当注意,只有同频的正弦量才能对相位进行比较,不同频率的正弦量无法确定领先、落后的关系,因此不能进行相位的比较,也不存在相位差。

【例3.1.5】　求下列两正弦电流的相位差:

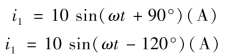
解　i1 与i2 的相位差

因相位差的绝对值规定不得大于180°,所以采用

即i1 滞后i2 150°,或i2 超前i1 150°。

【例3.1.6】　已知电路中某条支路的电压u 和电流i 为工频正弦量,它们的最大值分别为311 V、5 A,初相分别为π/6 和-π/3。 (1)试写出它们的解析式;(2)试求u 与i 的相位差,并说明它们之间的相位关系。

解

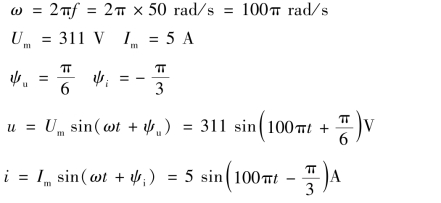
3)有效值

交流电的大小和方向都在随时间变化,为了能反映出不同波形的交流电在电路中能量转换的效果(如做功能力、发热量等) ,在比较它们的大小时使用有效值。

有效值是以交流电在一个或多个周期的平均效果作为衡量的指标,由于在电工技术中经常利用电流的热效应和机械效应,所以交流电的有效值这样定义:

交流电流i 通过电阻R 在一个周期T 内产生的热量QAC,如果与某一直流电流I 通过同一电阻在同一时间内所产生的热量QDC相等时,则称直流电流I 的数值是交流电流i 的有效值。

由此可知:

为使WAC =WDC,可得出i 的有效值为

有效值等于周期交流的平方在一个周期内的平均值的平方根,即等于周期交流的方均根值或均方根值。 有效值用大写字母来表示,如I、U、E 等。

对于正弦电流i=Im sin ωt,它的有效值为

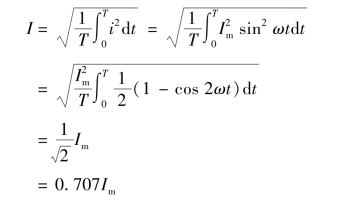
由此可知,正弦交流电流的有效值为最大值的2/2 倍。

同理可得,正弦交流电压的有效值为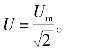

在交流电路中用电压表、电流表测量出来的电压、电流值,一般均是有效值。 在交流电路中使用的电器,其额定电压、电流大多也是有效值。

若用电流表测量正弦电路,电流表读数为10 A,可知该电流的最大值为我国工频交流电压值220 V 指的也是有效值,其最大值为

因此,根据正弦交流电有效值与幅值的数量关系,正弦交流电的表达式可表示为

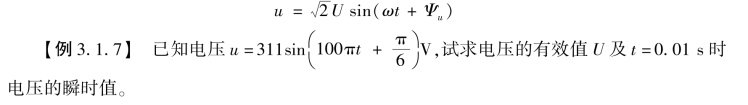
解(www.xing528.com)

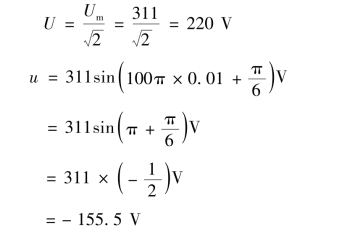
二、正弦量的表示方法

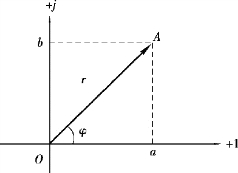
图3.1.4　复数

用函数或波形图来表示正弦量,这两种方式表示的正弦量难以进行加减运算。 因此,为了更方便地对正弦电流电路进行分析、计算,通常采用相量图或相量表示式(复数符号法) 来表示正弦量。

图3.1.4 为复数直角坐标系,横轴为复数的实部,纵轴为虚部。 图中的有向线段A 代表一相量。 复数有如下几种表示形式:

1)代数形式

A = a + jb

2)三角形式

A = r cos φ + jr sin φ

3)指数形式

A = rejφ

4)极坐标形式

A = r∠ψ

以上几种形式可以相互转换,进行加减运算可用代数形式,进行乘除运算可用指数形式或极坐标形式。

在分析正弦交流电路时,所有正弦电量的角频率ω 相同。 因此,在使用复数表示正弦量时,只需表示正弦量三要素当中的幅值(或有效值)与初相位即可。 用复数的幅值来表示正弦量的幅值(或有效值),用复数的辐角来表示正弦量的初相位。

为了与一般的相量区分开,一般采用相应物理量的大写字母来表示正弦交流电量的相量,同时在大写字母上加圆点,比如:

【例3.1.8】　用相量式表示以下正弦交流电流:(a)i=10 sin(ωt+30°)A;(b)i=5 2 sin

解

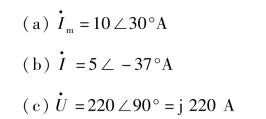
相量以图形表示时,称为相量图,如图3.1.5 所示,其长度代表正弦量的有效值或最大值,辐角代表初相,水平虚直线代表零度方向,在此方向的相量称为参考相量。

相量图包含了正弦交流电的有效值或最大值与初相位的信息,同时,画在同一张相量图中的各正弦量频率一定相同。

【例3.1.9】　试写出的相量表示式,并画出相量图。

解　i 的有效值I=10 A,初相Ψ= -30°,所以i 的相量表示式

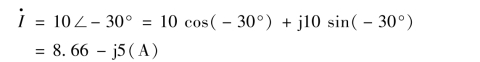
电流i 的相量图如图3.1.6 所示。

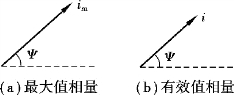
图3.1.5　正弦电流的相量

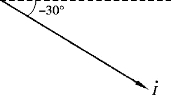
图3.1.6　【例3.1.9】图

三、正弦量的计算

设有两个同频率的正弦电流

i1 = I1msin(ωt + Ψ1)

i2 = I2msin(ωt + Ψ2)

根据三角函数的计算公式,可求得两同频率正弦电流相加之和的正弦电流频率不变,但幅值与相位都发生变化。

i = i1 + i2 = Im sin(ωt + Ψ)

确定合成电流i 的幅值Im 和初相Ψ,除通过三角函数计算公式外,还可用作图法与相量法来计算。

作图法:首先画出i1 和i2 的波形,而后将同一时刻的瞬时值叠加,逐点画出合成电流i的波形,如图3.1.7 所示,再测量出其最大值Im 和初相Ψ。 虽然这种方法比较直观,但作图不便,结果也欠准确,一般不采用。

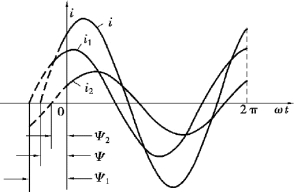
图3.1.7　作图法

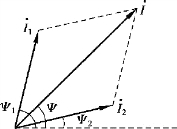
图3.1.8　相量法求和

【例3.1.10】　已知i1 =8 sin 314t A,i2 =6 sin(314t+90°)A。 (a)写出电流的相量式;(b)画出相量图;(c)求i=i1 +i2。

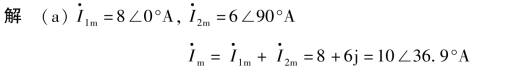
(b)相量图如图3.1.9 所示。

(c)i=10 sin(314t+36.9°)

【例3.1.11】　已知i1 =10 2 sin(ωt +90°)A,i2 =10 2 sin ωt A。 试用相量作图法求i =i1 +i2。

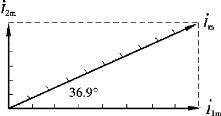
图3.1.9　【例3.1.10】图

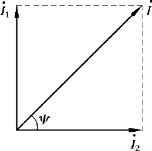
图3.1.10　【例3.1.11】图

应用相量法对正弦量进行减法时,实质上与加法相同,只需将作为减数的相量变成负相量后进行相加。 例如

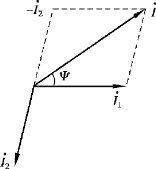
图3.1.11　【例3.1.12】图

故

i=i1 -i2 =8.66 2 sin(ωt+30°)(A)

相量图可以清楚地表示各正弦量的相互关系,又可得到所要分析的结果,所以相量图是分析正弦电路的重要工具。

下面讨论虚数单位j 在相量分析中的意义。

相量图如图3.1.13 所示。

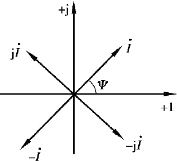
图3.1.12　旋转90°的算子j

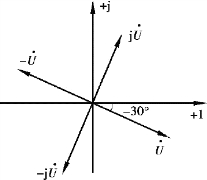
图3.1.13　【例3.1.13】图

正弦量用复数表示后,能适应各种运算的需要。 正弦电路的计算,常常采用复数来运算,配合相量图进行定性分析。

【例3.1.14】　已知i1 =10 sin(ωt+45°)A,i2 =5 2 sin(ωt-36.9°)A,求i=i1 +i2,并作相量图。

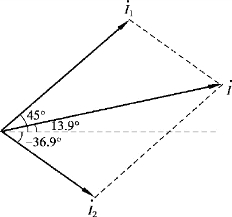
图3.1.14　【例3.1.14】图

解　先用相量的代数式表示i1 和i2:

相量图如图3.1.14 所示。

实践知识

【任务简介】

1)任务描述

(1)会测量交流电压、电流;

(2)学会使用万用表测量电压;

(3)学会计算功率与阻值。

2)任务要求

完成室内照明电路的电压电流测量,并计算阻值与功率。

3)实施条件

表3.1.1　室内照明电路的电流与电压的测量

【任务实施】

1)操作过程

按图3.1.15 接线,请老师检查后方可通电。

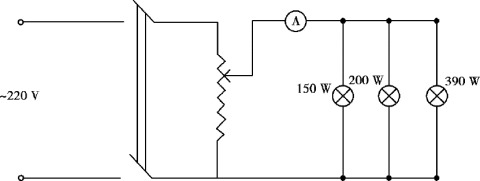
图3.1.15　实验电路图

2)数据记录

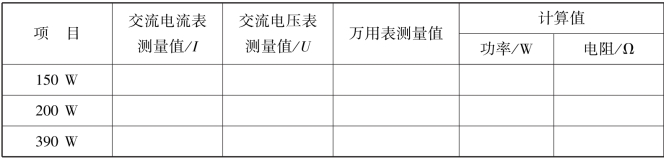
表3.1.2　数据记录

3)注意事项

电流表不能接错,否则会造成短路,调压器输入输出端不能接反。

4)思考题

写出所测各交流电流电压的表达式,并用相量式与相量图表示。

5)检查及评价

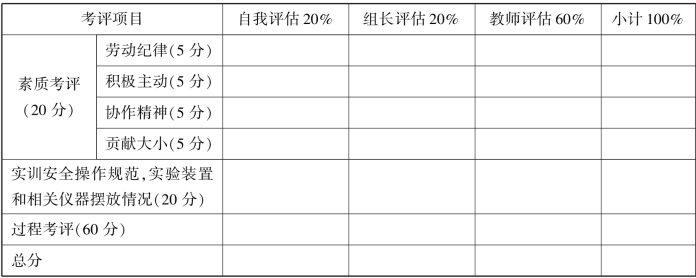
表3.1.3　检查与评价