基尔霍夫定律验证方法

【任务目标】

•知识目标

(1)掌握基尔霍夫电流定律和电压定律的概念;

(2)掌握电流、电压参考方向与实际方向的区别;

(3)通过支路电流法的学习,掌握电路网络中各个术语的含义。

•能力目标

(1)能识读电路图;

(2)能按图正确接线;

(3)能根据实验数据做出正确分析;

(4)能在实际电路中运用基尔霍夫电流、电压定律分析电路。

•态度目标

(1)能主动学习,在完成任务过程中发现问题、分析问题和解决问题;

(2)能与小组成员协商、交流配合完成本次学习任务,养成分工合作的团队意识;

(3)能养成严谨细致的作风,提高逻辑思维能力。

【任务描述】

通过验证实验,学习基尔霍夫定律,会用基尔霍夫定律进行复杂电路分析,班级学生自由组合为若干个实验小组,各实验小组自行选出组长,并明确各小组成员的角色。 在电工实验室中,各实验小组按照《Q/GDW 1799.1—2013 国家电网公司电力安全工作规程》、进网电工证相关标准的要求,进行基尔霍夫定律的验证实验。

【任务准备】

课前预习相关知识部分,独立回答下列问题:

(1)只有导线没有元件的一段电路算支路吗?

(2)基尔霍夫定律所描述的关系是否与电路元件的性质有关?

(3)KCL 体现了电路的什么重要规则?

(4)如何求解一个复杂电路的开口处电压?

【相关知识】

理论知识

电路元件的伏安关系反映元件本身的电压与电流关系,是元件上的电压与电流的约束关系。 在电路的分析当中,除了元件的约束关系之外,各支路和元件按不同的方式连接之后,各支路电压和各支路电流也存在着相互约束的关系。 基尔霍夫定律就是描述这些支路之间的电压和电流约束关系的基本定律,是德国科学家基尔霍夫在1845 年提出,它包含两条内容,分别为基尔霍夫电流定律和基尔霍夫电压定律。

一、常用电路术语

电路分析过程中,有许多专用的术语需要掌握。

1)平面电路

平面电路是可以画在一个平面上,而又没有任何两条支路在非节点处交叉的电路。 图2.1.1 所示电路就是平面电路。

2)支路

支路是电路中流过同一电流的每一个分支。 通过支路的电流称为支路电流,支路两个端点之间的电压称为支路电压。 图2.1.1 所示电路中有三条支路:acb、ab、adb。

3)节点

节点是电路中三条或三条以上支路的连接点。 图2.1.1 所示电路中有a 和b 两个节点。 在现代电路理论中,支路与支路之间的连接点,即元件之间的连接点,称为节点。 如此定义,图2.1.1 所示电路中a、b 均为节点。

4)回路

回路是电路中由若干条支路构成的闭合路径。 图2.1.1 所示电路中有三个回路:abca、adba、adbca。

5)网孔

在平面电路中,内部不存在支路的回路为网孔。 图2.1.1 所示电路中回路abca 和adba为网孔。

二、基尔霍夫电流定律(简称KCL)

基尔霍夫电流定律又称为基尔霍夫第一定律,它反映电路中任一节点的各支路电流的关系。

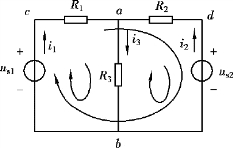
图2.1.1　基尔霍夫定律的说明

图2.1.2　KCL

图2.1.2 所示为电路的一个节点,支路电流I1 和I4、I5 流入节点,I2 和I3 从节点流出。KCL 指出,在任何时刻,流入节点的电流的总和等于从节点流出的电流的总和,用数学式表示为

I1 + I4 + I5 = I2 + I 3

如果把所有电流项移至等号左边,则有

I1 - I2 - I3 + I4 + I5 = 0

或写成

式(2.1.1)就是KCL 的表达式,内容为: 在任何时刻,连接于同一节点的各支路电流的代数和等于零。

KCL 适用于电路的节点,也可推广应用于电路中的任一假设封闭面。 如对图2.1.3 所示的封闭面S(也称为广义节点),可列写KCL 方程为

IA + IB + IC = 0

又如图2.1.4 中,两网络N1 和N2 之间只有一条导线相连,连线上的电流I 等于多少呢?我们只有一个封闭面S 包围住N2,再对封闭面列写KCL 为

I = 0

可见,两网络间的单根连线上没有电流。

KCL 体现了电路的一个重要的规则:电流是连续的,只能在闭合的回路中流动。

【例2.1.1】　求图2.1.5 所示电路中的i1 +i2 +i3 的数值。

图2.1.3　广义节点

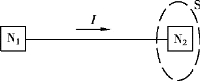
图2.1.4　两网络间的单根连线

解　对虚线所示封闭面列KCL 方程,得

I1 + I2 + I3 = 0

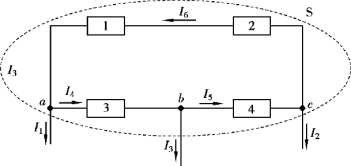
图2.1.5　【例2.1.1】图

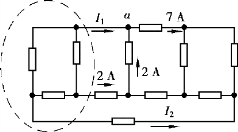
图2.1.6　【例2.1.2】图

【例2.1.2】　求图2.1.6 所示电路中的电流I1 和I2。

解　本题所涉及的基本定律就是基尔霍夫电流定律。 基尔霍夫电流定律对电路中的任意节点适用,对电路中的任何封闭面也适用。 本题就是KCL 对封闭面的应用。

对于节点a,有:I1 +2 -7 =0

对封闭面有:I1 +I2 +2 =0

I1 =7 -2 =5(A),I2 = -5 -2 = -7(A)

三、基尔霍夫电压定律(简称KVL)

基尔霍夫电压定律又称为基尔霍夫第二定律,简称KVL,是描述电路中任一回路中各元件电压之间关系的定律。

图2.1.7　KVL

图2.1.7 所示为复杂电路中的一个回路(其他部分未画出),如果从a 点出发,沿a—b—c—d—a 绕行时,电位有时降低,有时升高。 但绕行一周,回到出发点a,电位的数值不会改变。 也就是说,沿回路绕行一周,电压降的总和等于电压升的总和,即

u1 + u4 = u2 + u3

若把所有的电压项都移至等号左边,则有

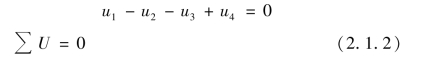
写成一般式为

基尔霍夫电压定律可以表述为: 任一时刻,沿电路任一回路的所有元件电压的代数和等于零,即式(2.1.2)就是KVL 的表达式。

列写KVL 方程应该注意以下两点:

(1)列写KVL 方程时,要确定“代数和”中的正负号。

(2)确定正负号的方法如下:任意选定一回路绕行方向(或称回路参考方向,一般取顺时针方向),凡支路电压的参考方向与回路的绕行方向一致者,电压前面取“ +”号;凡支路电压的参考方向与回路的绕行方向相反者,电压前面取“ -”号。

【例2.1.3】　在图2.1.8 所示的电路中,对各回路列写KVL 方程。

解　通常,电路中的电阻电压由电阻及其电流的乘积表示,则图2.1.7 对应KVL 方程也可以表示为

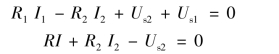
【例2.1.4】　在图2.1.9 所示电路中,若以f 点作为参考点,试计算c、d 两点的电位。

解　5 Ω 支路上电流为零。

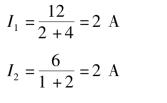
Vc =Ucf =Uaf +Uba +Ucb =12 -2 ×2 +0 =8 V

Vd =Udf =Udc +Ucb +Uba +Uaf =2 ×1 +0 -2 ×2 +12 =10 V

图2.1.8　【例2.1.3】图

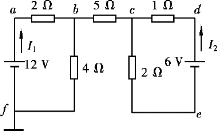
图2.1.9　【例2.1.4】图

使用基尔霍夫定律列写方程时应该注意的要点:

(1)n 个节点可以列写出n 个KCL 方程,但只有n-1 个方程具有独立性。

(2)L 个回路可以列写L 个KVL 方程,但只有b-n+1 个KVL 方程具有独立性(b 为支路数)。

(3)基尔霍夫定律用于集总参数的线性和非线性电路。 定律列写的方程仅与电路结构有关,与元件性质无关。

基尔霍夫定律具有普遍的适用性,与电路元件的性质无关。 它适合于有任何元件所构成的任何结构的电路,电路中的电压和电流可以是恒定的,也可以是任意变化的,但不适合于分布参数电路。

四、支路电流法

在分析计算复杂电路时,单独运用欧姆定律、基尔霍夫电压定律或基尔霍夫电流定律,往往很难直接求得电路的电压和电流。 那么,能否找到一些普遍适用于复杂电路的电路分析方法呢? 答案是肯定的。

支路电流法就是计算复杂电路的方法中的一种最基本的方法。 所谓支路电流法,就是以支路电流为待求量,根据基尔霍夫电流定律和基尔霍夫电压定律,分别列出电路的节点电流方程和回路电压方程,然后联立求解方程组,从而求出未知量的一种方法。

下面通过对图2.1.10 所示电路的分析,介绍支路电流法的思路和解题步骤。 图中电压源和电阻已给定,任意选定三个支路电流的参考方向并标在图中。

应用KCL,对节点a 和b 列出电流方程为

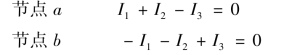
两个方程相差一个负号,说明只有一个方程是独立的。

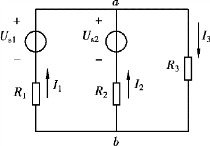
图2.1.10　支路电流法

结论:(www.xing528.com)

对于具有n 个节点的电路,其独立KCL 方程的数目为(n-1)个。

应用KVL,对三个回路列出电压方程

左网孔　R1I1 -R2I2 =Us1 -Us2

右网孔　R2I2 + R3I3 =Us2

大回路　R1I1 + R3I3 =Us1

结论:

对具有b 条支路、n 个节点的电路应用KVL,能够且只能够列出b -(n -1)个独立的KVL 方程。

对于平面电路,选择网孔作为独立回路。

选择上述三个独立的方程,联立求解即可得出各支路电流。

结合上面的分析,利用支路电流法求解电路各支路电流的一般步骤是:

(1)确定电路的支路数b、节点数n 和独立回路数l;

(2)标出各支路电流的参考方向;

(3)对电路中n-1 个独立节点应用KCL,列出节点电流方程;

(4)选取b-n+1 个独立回路(网孔),应用KVL 列出网孔电压方程;

(5)联立求解上述b 个独立方程,求得各支路电流;

(6)代入原方程组,检验计算结果。

支路电流法的优点在于思路清晰,方法简单;缺点在于当支路数较多的时候,方程数量多,计算繁琐。 现举例说明解题过程。

【例2.1.5】　如图2.1.11 所示,已知:E1 =15 V,E2 =65 V,R1 =5 Ω,R2 =R3 =10 Ω。试用支路电流法求R1、R2 和R3 三个电阻上的电压。

解　在电路图上标出各支路电流的参考方向,如图所示,选取绕行方向。 应用KCL 和KVL 列方程如下

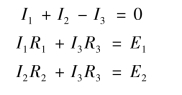
代入已知数据得

解方程可得:

三个电阻上的电压电流方向选取一致,则三个电阻上的电压分别为

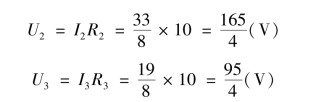
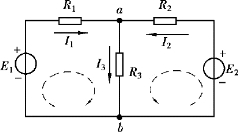
图2.1.11　【例2.1.5】图

图2.1.12　【例2.1.6】图

【例2.1.6】　用支路电流法求示图2.1.12 电路中各支路电流。

解　方法一:增设电流源电压为未知变量。

(a)设电路中的电流源电压为U,支路电流分别为I1、I2、I3;选择它们的参考方向选择如图所示。

(b)根据电流的参考方向,确定电流源所在支路的电流为I2 =IS =3 A。

(c)对电路中的独立节点b 应用KCL,得

I1 + I2 + I3 = 0

(d)选择网孔作为独立回路,选择回路绕行方向如图所示,对两网孔应用KVL,得

2I1 -4I2 + U = 24

4I2 - I3 - U = -12

(e)联立求解上述方程

求得:

I1 = 3 A,I2 = 3 A,I3 = -6 A

方法二:避开电流源所在支路,选择不含电流源的回路作为独立回路,列写KVL 方程。

(a)根据电流的参考方向,确定电流源所在支路的电流为

I2 = IS = 3 A

(b)对电路中独立节点b 应用KCL,列写KCL 方程为

I1 + I2 + I3 = 0

(c)对电路中不含电流源的独立回路abcda 应用KVL,列写KVL 方程为

2I1 - I3 +12 -24 = 0

(d)联立求解上述方程求得

I1 = 3 A,I2 = 3 A,I3 = -6 A

五、节点电压法

支路电流法解题时同时应用了KCL 和KVL,如果在引入变量的时候,使引入的变量先满足KVL,就只需列关于变量的KVL 方程即可,而节点电压法的思路与此类似。

电路中,如果任选一个节点作为参考点,则其他节点到参考点之间的电压称为该节点的节点电压。 以节点电压为未知量,应用KCL 写出各独立节点的节点电流方程,从而求解电路的方法,称作节点电压法,简称节点法。 节点电压法适用于支路数很多而节点个数相对较少的电路,尤其是当电路只有两个节点时,用节点电压法尤为方便快捷。 对于只有两个节点的电路可用弥尔曼定理求解。

如图2.1.13 所示的电路中,只有两个节点①和②,选②为参考点,则①的节点电压Un1 =U12(n 表示节点)。 在给定电源电压和电阻的情况下,如果求出节点电压Un1,再计算各支路电流就很容易。

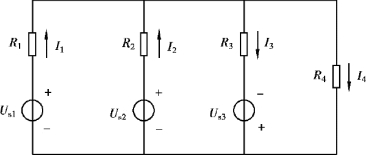
图2.1.13　具有两个节点的电路

节点电压与支路电流的关系是

前三个式子的分子部分均为各支路的电阻电压,故三式为含源支路的伏安关系式。 而各支路电流受KCL 约束,即

I1 + I2 - I3 - I4 = 0

将式(2.1.3)代入上式,并经整理可得

这就是计算节点电压的公式,推广到一般情况

在式(2.1.5)中,分子实际上是代数和,凡参考方向是指向非参考节点的电流源电流IS前面取“ +”号,反之取“ -”号;凡是Us 的参考方向与节点电压的参考方向一致的取“ +”号,相反的取“ -”号。 式(2.1.6)也称为弥尔曼定理。

【例2.1.7】　应用弥尔曼定理计算图2.1.14 所示电路中各支路电流。

解

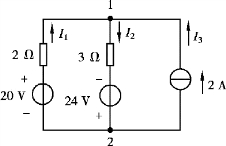
图2.1.14　【例2.1.7】图

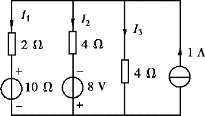
图2.1.15　【例2.1.8】图

【例2.1.8】　应用节点电压法求图2.1.15 所示电路中各支路电流。

解　各节点电压参考方向如图中所示,根据弥尔曼定理得

得

如果电路的支路数很多,而节点只有两个时,采用弥尔曼定理求解将非常简单。 弥尔曼定理只适用于计算两个节点的电路,而节点电压法适用于3 个或3 个以上节点的电路。

实践知识

【任务简介】

1)任务描述

(1)掌握KCL,KVL 定律的验证;

(2)学会接线与实际操作,加深对参考方向的理解。

2)任务要求

按实验接线图正确接线,经指导教师检查确认后合电源开关,分别测量各支路电流和回路电压,根据测量数据验证基尔霍夫电流、电压定律。

3)实施条件

表2.1.1　基尔霍夫定律的验证

【任务实施】

1)电路图

2)操作步骤

(1)按图2.1.16 接线。

(2)经老师检查电路后,合上开关K1、K2、K3,测量流入节点C 的电流I1 及流出节点C的电流I2、I3,验证KCL。 将数据记录入表2.1.2 中。

图2.1.16　电路图

(3)分别测量abcda、dcefd、abefa 三个回路各段电压降,验证KVL。 将数据记入表2.1.2中。

3)数据记录

表2.1.2

续表

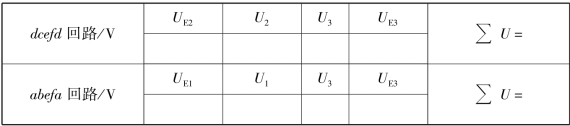
4)注意事项

(1)测各段电压降,使电压由正指负的方向与所选各电压正方向一致。 此时,若指针正偏,则该电压取正;若指针反偏,则调换电压表正负端钮。 此时,指针正偏则该电压取负值。

(2)测U1、U2、U3 时,必须将电流表的压降包括进去,否则误差太大。

5)思考题

测量时能否任意选定电流和电压的参考方向,其结果如何? 不选参考方向行不行?

6)检查及评价

表2.1.3　检查与评价