1.等分线段（图3-20）
（1）作直线AC与已知线段AB成20°～40°角度。
（2）由A点起在AC上任意截取五等分点a、b、c、d、e。
（3）连接Be，过d、c、b、a点分别作Be的平行线。在AB上的交点d′、c′、b′、a′即为线段AB的五等分点。
2.作与线段定距离的平行线（图3-21）
（1）在已知线段AB上任意取两点a、b。
（2）分别以a、b为圆心，R为半径在线段AB的同侧划弧（R为给定距离）。
（3）作两弧的切线，即为所求的平行线。
图3-20 等分线段
图3-21 作与线段定距离的平行线
3.过线外一点P作该线的平行线（图3-22）
（1）在线段AB的中段任取一点O。
（2）以O为圆心、OP为半径作弧、交AB于点a、b。
（3）以b为圆心，AP为半径作弧，交ab弧于点c。
（4）连接Pc，即为所求平行线。
4.在已知线段的端点作垂线（图3-23）
（1）以B为圆心，取Ba为半径作圆弧，交线段AB于a点。
（2）其长度为aB，在圆弧上截取
（3）以b、c为圆心，Ba为半径作圆弧，得交点d，连接dB，即为所求垂线。
图3-22 过线外一点作该线平行线
图3-23 在已知线段的端点作垂线
5.求已知弧的圆心（图3-24）
（1）在已知圆弧
上截取N1N2和M1M2，并分别作线段N1N2和M1M2的垂直平分线。
（2）两垂直平分线的交点O即为圆弧AB的圆心。
6.作圆弧与两条相交的直线相切（图3-25）
（1）在两条相交直线的锐角∠BAC内侧，作与两直线相距为R的两条平行线，得交点O。
（2）以O为圆心、R为半径作圆弧，该圆弧即为所求。
图3-24 求已知弧的圆心
图3-25 作圆弧与两条相交直线相切
7.作圆弧与两圆外切（图3-26）
（1）分别以O1和O2为圆心，以R1+R及R2+R为半径，作圆弧交于O点。
（2）连接O1O交已知圆于M点，连接O2O交已知圆于N点。
（3）以O为圆心、R为半径作圆弧，该圆弧即为所求。
8.作圆弧与两圆内切（图3-27）
（1）分别以O1和O2为圆心，R—R1和R—R2为半径，作圆弧交于O点。
（2）以O为圆心、R为半径作圆弧，该圆弧即为所求。
图3-26 作圆弧与两圆外切
图3-27 作圆弧与两圆内切
9.等分圆周（图3-28）
（1）过圆心O作直径CD⊥AB。
（2）取OA的中点E。
（3）以E为圆心、EC为半径作圆弧交AB于F点，CF即为圆五等分的边长。
10.任意等分半圆（图3-29）
（1）将圆的直径AB分为任意等份（图中为五等份），等点为1、2、3、4。
（2）分别以A、B为圆心，AB长为半径作圆弧交于O点。(www.xing528.com)
（3）连接O1、O2、O3、O4并分别延长交半圆于1′、2′、3′、4′，这四点即为半圆等分点。
图3-28 等分圆周
图3-29 任意等分半圆
11.椭圆的画法
如图3-30所示，已知长轴ab，短轴cd，作椭圆。
（1）作ab垂直于cd。
（2）用直线连接a点和c点，以O点为圆心、Oa为半径作圆弧，交Oc的延长线于e点。
（3）以c点为圆心，ce为半径作圆弧，交ac于f点。
（4）作af的垂直平分线，交ab于1点，交短轴于2点，再与这两点对称，定出3点和4点。
（5）分别以1、2、3、4点为圆心，a1、c2、b3、d4为半径作圆弧，在切点的地方相接，就可以画成椭圆。
12.卵圆的画法（图3-31）
（1）作线段CD线垂直于AB，相交于O点。
（2）以O为圆心，OC为半径作圆，交AB于G点。
（3）分别以D、C为圆心，DC为半径作弧，交于e点。
（4）连接DG、CG并延长，分别交弧于E、F点。
（5）以G为圆心，GE为半径作弧，即得卵圆。
图3-30 椭圆的画法
图3-31 卵圆的画法
13.按同一弦长等分圆周
按同一弦长等分圆周就是用圆规按每一等分圆周对应的弦长来等分圆，主要是如何确定各等分圆周对应的同一弦长，如图3-32所示。
图3-32 按同一弦长等分圆周
设圆的直径为D，半径为R，若圆周作n等分，则每等份弧长所对的圆心角α=360/n，由三角形关系可求得：
所以弦长为
【例3-3】 在直径为80mm的圆周上作十等分。
用圆规量取尺寸24.72mm划线，就可以对圆周作十等分。
如果令上式的2sin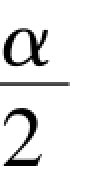
=K（K称作弦长系数），则弦长L=KR，K可按各种等分数预先算出，见表3-3，这样求弦长更方便。
表3-3 等分圆周弦长系数K
在例3-3中，当n=10时，查表得K=0.6180，则L=0.6180×40=24.72mm。
按同一弦长作圆周等分的方法，由于量规在量取尺寸时难免有误差，再加上划等分圆弧时圆规脚位置可能会变动产生误差，结果往往不能一次就使等分准确。等分数越多，其积累误差越大。因此，一般需要重新调整圆规尺寸后再作等分，直到等分准确。用这种方法等分圆周，其效率和准确性都不高。
14.按不等弦长等分圆周
如图3-33所示，用圆规按不等弦长对圆周作等分时，主要问题是如何确定各等分段的不等弦长Aa1、Aa2、Aa3、…设圆周作n等分，则按不等弦长等分时，其相应的不等弦长所对的圆心角分别为α、2α、3α、…其中，α=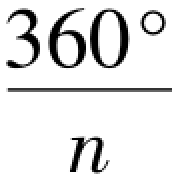
°。
图3-33 按不等弦长等分圆周
（a）等分原理；（b）偶数等分；（c）奇数等分
由三角关系可求得：
如图3-33（b）所示，当等分数为偶数时，为了等分方便，可先将圆周作两等分，然后按求得的各不等弦长，用圆规分别以A、B两点为圆心，依次在圆周上截取各等分点。如图3-33（b）中等分数为14，其中Aa1=Aa2=Bb1=Bb2，Aa3=Aa4=Bb3=Bb4，Aa5=Aa6=Bb5=Bb6。
【例3-4】 在直径为50mm的圆周上作14等分。
解 圆心角
为了等分方便，先将圆周作两等分，再对二分之一圆周作七等分即可。如图3-33（b）所示，只需求出三个不等弦长，即：
用圆规分别量取三种弦长，并分别以圆周两等分点A、B为圆心，依次划出各等分点，校对无误，则圆周等分完成。
当等分数为奇数时，可设法在圆周上先划出一个等分段，如图3-33（c）中的A′A″，剩下的等分数便为偶数，这时就可按例3-4的偶数等分法进行。为了偶数等分方便，要把圆周先作两等分，所以在划取等分段A′A″时，最好先求得A点，使AA′=AA″，显然，AA′=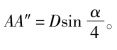
再按求得的各不等弦长，用圆规分别以A′、A″、B三点为圆心，依次在圆周上截取各等分点。图3-33（c）所示为11等分，其中A′a1=A″a2=Bb1=Bb2，A′a3=A″a4=Bb3=Bb4。
【例3-5】 在直径为50mm的圆周上作11等分。
用圆规先按AA′弦长在圆周上截取AA′和AA″，则A′A″为一个等分段；然后用圆规按两种不等弦长，分别以圆周上的A′、A″、B三点为圆心，依次划出各等分点。校核无误，则等分圆周完成。
用不等弦长法对圆周作等分时，虽然计算工作量稍有增加，但可避免操作中产生的累积误差，还能较迅速和准确地进行等分。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
