红外光谱是由于分子振动能级的跃迁(同时伴随转动能级的跃迁)而产生的。
物质吸收电磁辐射应满足两个条件:辐射应具有刚好能满足物质跃迁时所需的能量,即分子中某个基团的振动频率和外界红外辐射的频率一致;辐射与物质之间有耦合(coupling)作用,即外界辐射可将能量迁移到分子中去。这种能量转移是通过偶极矩(dipole moment)的变化来实现的,这可用图6-1的示意简图来说明。当辐射频率与偶极子频率相匹配时,分子才与辐射发生相互作用(耦合振动)而增加它的振动能,使振动的振幅增加,分子由原来的基态振动跃迁到较高的振动能级。可见,并非所有的振动都会产生红外吸收,只有发生偶极矩变化的振动才能引起可观测的红外吸收谱带,这种振动称为红外吸收(infrared active),反之称为非红外吸收(infrared inactive)。

图6-1 偶极子在交变电场中的作用示意图
用频率连续改变的红外光照射某样品时,该试样对不同频率的红外光进行吸收。将通过样品的红外光情况用仪器记录,就得到该试样的红外吸收光谱图。
1.影响吸收峰强度的因素 红外光谱吸收峰的强度主要由两个因素决定。其一,能级跃迁的概率。基频跃迁概率大,吸收峰较强;倍频跃迁概率低,故倍频谱带很弱。其二,分子振动时偶极矩变化的程度。根据量子理论,红外光谱的强度与分子振动时偶极矩变化的平方成正比。如C=C的吸收峰强度较弱,C=O的吸收峰很强。
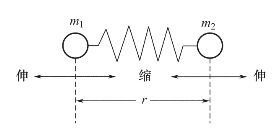
图6-2 谐振子振动示意图
2.分子振动方程式 分子由原子组成,故可以将多原子分子看作是由双原子分子构成的集合体。
根据经典力学理论,可以把组成双原子分子的两个原子看作是用弹簧连接的两个刚性小球。假设弹簧的质量忽略不计,这样两个原子沿着键轴方向的振动可以近似地看作是简谐振动,如图6-2所示。
根据胡克定律,体系的振动频率σ(以波数表示)为:

式中:c——光速(2.998×1010cm/s);
k——弹簧的力常数(force constant),N/cm;
μ——两个小球(即两个原子)的折合质量,g。

其中 m1、m2分别代表两个小球的质量。
式(6-5)所示的双原子分子的振动频率可进一步简化为:
![]()
由式(6-7)可见,有机化合物分子发生振动能级跃迁需要的能量大小取决于化学键两端原子的折合相对原子质量和化学键的力常数,即取决于分子本身的结构特征。一些化学键的力常数见表6-2。
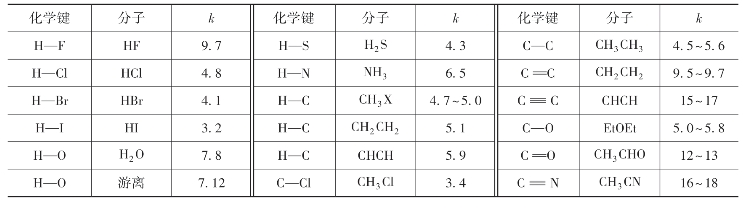
表6-2 某些化学键的力常数K 单位:N/cm
例[6-1],试计算CH3CHO中C=O的振动频率。
解:查表6-2,C=O的力常数k为12~13N/cm,取12N/cm代入式(6-7):(https://www.xing528.com)
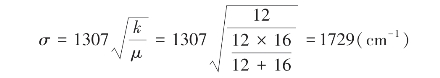
官能团C=O的振动频率为1729cm-1。
醛类化合物中的C=O的振动频率通常为1725cm-1。
由于组成分子的各原子之间的相互作用错综复杂,对各官能团的振动频率有不同程度的影响,故官能团的计算值与实际测定值略有差异。
红外光谱的基本原理用英文描述如下:
All molecules are made up of atoms linked by chemical bonds.The movement of atoms and chemical bonds can be likened to that of a system comprised of springs and balls in constant motion.Their motion can be regarded as being composed of two components,the stretching and bending vibration.The frequencies of these vibrations are not only dependent on the nature of the particular bonds themselves,such as the C—H or C—O bonds,but are also affected by the entire molecule and its environment.This situation is similar to that encountered in the springball system in which the vibration of a single spring is under the influence of the rest of the system.“The internal motion of this system will become greater if energy is transferred to it.”
Similarly,the vibrations of bonds,which accompany electric vibrations,will increase their amplitude if an electromagnetic wave (infrared beam) strikes them.The difference between a molecule and the spring ball system is that the vibrational energy levels of the former are quantized;therefore,only the infrared beam with a frequency exactly corresponding to that required to raise the energy level of a bond will be absorbed,viz.,the amplitude of the particular vibration is increased suddenly by a certain amount and not gradually.When the sample is irradiated by an infrared beam whose frequency is changed continuously,the molecule will absorb certain frequencies as the energy is consumed in stretching or bending different bonds.The transmitted beam corresponding to the region of absorption will naturally be weakened,and thus a recording or the intensity of the transmitted infrared beam versus wave-numbers or wavelength will give a curve showing absorption bands.This is the infrared spectrum.
3.分子振动的类型与吸收峰 多原子分子的振动可分为伸缩(stretching)振动和变形(bending)振动两种,如图6-3所示。

图6-3 亚甲基的振动类型与各种振动方式(“+”表示向前运动,“—”表示向后运动)
伸缩振动是指原子沿化学键的键轴方向伸展和收缩(用ν表示振动频率),振动时键长发生变化而键角不变。伸缩振动有对称伸缩(νs)和不对称伸缩(νas)两种。对于同一基团,不对称伸缩振动的频率要稍高于对称伸缩振动频率。
变形振动又称弯曲振动,是指原子间键角发生周期性变化的一种振动,而键的长度不变,用δ表示。弯曲振动包括面内(in-plane)弯曲和面外(out-of-plane)弯曲两种。面内弯曲振动又分为简式振动和摇摆振动,面外弯曲振动又分为面外摇摆和扭曲振动。
红外光谱中,分子出现的吸收峰多少与分子的总体振动形式有关。多原子分子简谐振动的数目称为振动自由度(degree of freedom),每个振动自由度对应红外光谱图上的一个基频吸收带。由N个原子组成的分子,其振动自由度=3N-(平动自由度+转动自由度)。对于非线型分子,振动形式有f=3N-6种。对于直线型分子,若贯穿原有原子的轴在X方向,则直线型分子的振动形式为f=3N-5种。
例如,水分子为非线型分子,f=3N-6=3,故水分子有3种振动形式,如图6-4所示。二氧化碳分子为线型分子,f=3N-5=4,有4种振动形式,如图6-5所示。
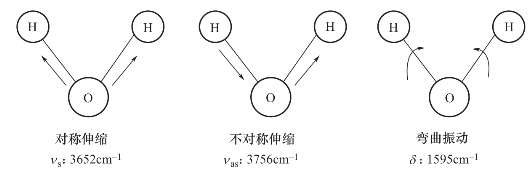
图6-4 水分子的振动及其红外谱图
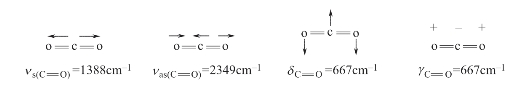
图6-5 二氧化碳分子的基本振动方式及其红外谱图
大多数分子的红外光谱基频吸收峰可以用振动自由度f来推测,但实际上红外光谱观察到的吸收峰数目有时会增多或减小。这主要是由以下因素造成的。
(1)非红外活性振动。如二氧化碳分子,计算所得f=3×3-5=4,但对称伸缩偶极矩总变化μ=0,正负电荷中心重合,无峰,只有在2349cm-1处出现反对称伸缩吸收峰。
(2)峰的简并。频率相同的振动只出现一个峰,如二氧化碳分子在667cm-1处的吸收峰。
(3)弱峰被强峰覆盖或太弱,观察不到。
(4)吸收峰不在检测器范围内。
(5)由于振动耦合及费米效应,使相应吸收峰分裂为两个峰。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




