如何进行DMA分析及其应用

试样在周期性（正弦）变化的机械振动应力作用下会发生相应的振动应变。测得的应变往往滞后于所施加的应力，除非试样是完全弹性的，这种滞后称为相位差，即相角δ差。

测试中，施加在试样上的应力必须在胡克定律定义的线性范围内，即应力—应变曲线起始的线性范围。DMA分析可以测试样品应力的振幅、应变的振幅、应力与应变间的相位差。

1.力和位移　在样品上直接施加力后，样品会产生相应的位移。周期性变化的力F（t）为：

式中：FA——力的振幅；

ω——角频率；

f——振动频率。

样品发生的位移L（t）：

式中：LA——位移的振幅；

δ——位移对于力的相位移。

2.刚度和模量　力和位移之比称为刚度，它与试样的几何形状有关。

归一化到面积A上的力称为机械应力或应力σ（单位面积上的力），归一化到原始长度L0的位移称为相对形变或应变ε。应力与应变之比称为模量，模量与试样的几何形状无关。

3.几何因子　在动态力学分析中，用力的振幅FA和位移的振幅LA来计算复合模量。而几何因子由刚度和模量计算得到。

拉伸或压缩实验的弹性模量E*为：

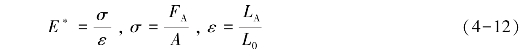
进一步转换为：

为刚度，所以弹性模量的计算公式可变为：

各种动态热机械测量模式及其几何因子的计算公式见表4-5。

表4-5　DMA测量模式及其试样几何因子的计算公式

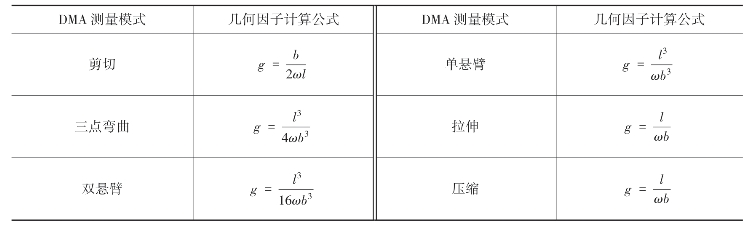
注　b为厚度，ω为宽度，l为长度。

4.复合模量、储能模量、损耗模量和损耗角　DMA可以测量样品的复合模量M*。复合模量由同相分量M′（或以G′表示，称为储能模量）和异相（相位差π/2）分量M″（或以G″表示，称为损耗模量）组成。损耗模量与储能模量之比M″/M′=tanδ，称为损耗因子（或阻尼因子）。

复合模量M*、储能模量M′、损耗模量M″和损耗角δ之间的关系可用图4-30所示的三角形表示。

储能模量M′与应力作用过程中储存于试样中的机械能量成正比。损耗模量表示为应力作用过程中试样所消散的能量（损耗为热）。损耗模量大表示黏性大，因而阻尼强。损耗因子tanδ等于黏性与弹性之比，损耗因子大表示能量消散程度高，黏性形变程度高。它是每个形变周期耗散为热的能量量度。损耗因子与几何因子无关，因此即使试样几何状态不好，也能精确测定。

(www.xing528.com)

图4-30　复合模量示意图

模量的倒数称为柔量。与模量相对应，柔量有复合柔量、储能柔量和损耗柔量。在描述材料力学性能时，复合模量与复合柔量是等效的。

通常情况下，试样可表现为3种类型的应力—应变行为。

（1）纯弹性。应力与应变同相，即相角δ为0。纯弹性样品在振动时没有能量损失。

（2）纯黏性。应力与应变异相，即相角δ为π/2。纯黏性样品在振动时能量完全转变为热。

（3）黏弹性。形变对应力响应有一定的滞后，即相角δ在0～π/2之间。相角越大，振动阻尼越强。

图4-31为黏弹性样品在频率f为1Hz下的DMA曲线。试样的正弦形变是对正弦应力的反应。形变对力的响应有一个时间滞后Δ，也可用相角δ表示，δ=2πfΔ。DMA曲线物理量计算见表4-6。

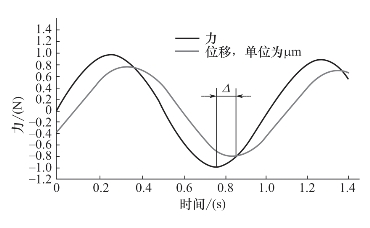
图4-31　黏弹性样品的DMA曲线

表4-6　黏弹性样品的DMA曲线物理量计算

5.温度—频率等效原理　在应力作用下，行为线性（弹性模量与力或位移振幅无关）的各向同性黏弹性材料，适用下述的温度—频率等效原理。

在恒定负载下，分子发生缓慢重排使应力降至最低，材料因此随时间进程发生形变；如果施加振动应力，由于可用于重排的时间减少，所以应变随频率增大而下降。因此，样品在高频下比在低频下更坚硬，即模量随频率增大而增大。随着温度增加，分子重排的速度加快，因此位移振幅增大，等同于模量下降；在一定频率下，在室温下测得的模量与在较高温度、较高频率下测得的模量相等。这就是说，频率和温度以互补的方式影响材料的性能，这就是温度—频率等效原理。因为频率低的效果与延长时间的效果相同，反之亦然，所以温度—频率等效又称为时间—温度叠加（time-temperature superposition，TTS）原理。

运用温度—频率等效原理，可获得实验无法直接达到的频率的模量信息。例如，室温下，由于DMA的频率上限达不到几千赫兹，因而橡胶共混物的阻尼行为无法由实验直接测试，但可借助温度—频率等效原理，用低温和可测频率范围进行的测试，将室温下的损耗因子外推至几千赫兹。温度—频率等效原理可用WLF（Williams-Landel-Ferry）方程式或Vogel-Fulcher方程式描述，两个方程是等价的。

WLF方程表达式为：

式中：Tr——任意参比温度；

fr——与Tr对应的参比频率；

C1、C2——WLF常数，该值与参比值的选择有关。

Vogel-Fulcher方程表达式为：

式中：f0——频率上限；

Tv——Vogel温度；

B——曲率参数。

图4-32为温度—频率等效原理应用于聚合物的图示说明。左边曲线为1Hz下玻璃化转变区储能模量与温度的关系，右边曲线为同一聚合物在室温下测量的储能模量与频率的关系。以对数表示频率，两条曲线呈镜像。图4-32最上面的虚线直线表示在低温和高频下的相同模量，中间的虚线直线表示同一测试条件下中温和中频的相同模量，下面的虚线直线表示在高温和低频下的相同模量。

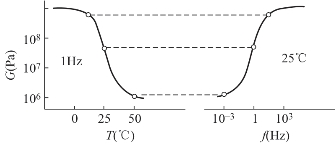
图4-32　温度—频率等效原理示意图