逻辑代数及其应用

1.2.1　基本逻辑门电路

逻辑门是数字电路的基本单元。一个逻辑门有一个输出端和一个或多个输入端。输出端只有1或0两种状态，或者说只有高电平和低电平两种状态，这取决于输入的信号和逻辑门的功能。逻辑门可进行与、或、非等逻辑运算，对应的也就有与门、或门、非门等基本逻辑门和基本逻辑门电路。

1.与逻辑和与门电路

当决定一件事的所有条件都满足时，该件事才会发生，这种因果逻辑关系称为与逻辑。描述与逻辑关系的模型电路如图8－2所示。

图8－2　与逻辑电路

逻辑假定为：变量中用1来表示开关闭合，用0表示开关断开；函数中用1来表示灯亮，用0表示灯灭，则可得到与逻辑真值表（即将输入、输出状态全部放到一张表格内），见表8－2。

表8－2　与逻辑真值表

与运算也称“逻辑乘”。逻辑乘的表达式为

在数字电路中，凡输入和输出之间符合与运算关系的我们称它为与逻辑电路，也称为“与门电路”，简称“与门”，其符号如图8－3所示。

图8－3　与逻辑符号

与逻辑功能为：输入有0，输出为0；输入全1，输出为1。

根据与门的逻辑功能，还可画出输入与输出间的波形，如图8－4所示。该图直观地描述了任意时刻输入与输出之间的对应关系及变化的情况。

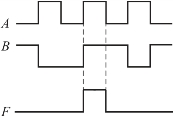
图8－4　与门波形图

2.或逻辑和或门电路

当决定事物结果的几个条件中，只要有一个或一个以上条件得到满足，结果就会发生，这种逻辑关系称为或逻辑关系。描述或逻辑关系的模型电路如图8－5所示。

图8－5　或逻辑电路

逻辑假定为：变量中用1来表示开关闭合，用0表示开关断开；函数中用1来表示灯亮，用0表示灯灭，则可得到或逻辑真值表，见表8－3。

表8－3　或逻辑真值表

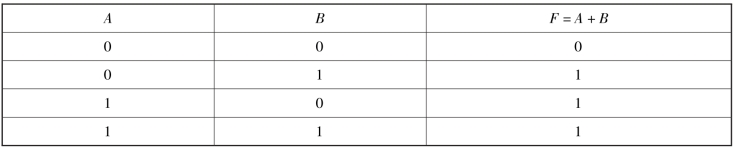
或运算也称“逻辑加”。逻辑加的表达式为

在数字电路中，凡输入和输出之间符合或运算关系的我们称它为或逻辑电路，也称为“或门电路”，简称“或门”。其符号如图8－6所示。

图8－6　或逻辑符号

或逻辑功能为：输入有1，输出为1；输入全0，输出为0。

根据或门的逻辑功能，还可画出输入与输出间的波形，如图8－7所示。该图直观地描述了任意时刻输入与输出之间的对应关系及变化的情况。

图8－7　或门波形图

3.非逻辑和非门电路

“非逻辑”又称“逻辑非”，或者叫“逻辑反”。决定事物的结果与条件刚好相反，这种逻辑关系称为非逻辑关系。描述非逻辑关系的模型电路如图8－8所示。

图8－8　非逻辑电路

逻辑假定为：变量中用1来表示开关闭合，用0表示开关断开；函数中用1来表示灯亮，用0表示灯灭，则可得到非逻辑真值表，见表8－4。

表8－4　非逻辑真值表

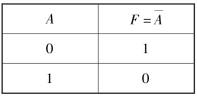
非运算也称“逻辑反”。逻辑反的表达式为

在数字电路中，凡输入和输出之间符合非运算关系的我们称它为非逻辑电路，也称为“非门电路”，简称“非门”。由于输入输出总是反相，所以通常也把非门叫作反相器。其符号如图8－9所示。

图8－9　非逻辑符号

非逻辑功能为：输入是1，输出为0；输入是0，输出为1。

根据非门的逻辑功能，还可画出输入与输出间的波形，如图8－10所示。

图8－10　非门波形图

1.2.2　复合逻辑门电路

用“与”“或”“非”三种基本逻辑运算的各种不同组合可以构成“与非”“或非”“异或”“同或”等复合逻辑，并构成相应的“复合门”。

1.与非门

将“与门”和“非门”组合在一起可以构成“与非门”，或称“与非逻辑”。一个与非门有两个或两个以上的输入端和一个输出端，图8－11所示为两输入端与非门的逻辑符号，逻辑函数表达式为

图8－11　两输入端与非门逻辑符号

与非门的真值表见表8－5。

表8－5　与非门的真值表

与非逻辑功能为：输入有0，输出为1；输入全1，输出为0。

2.或非门

将“或门”和“非门”组合在一起可以构成“或非门”，或称“或非逻辑”。一个或非门有两个或两个以上的输入端和一个输出端，图8－12所示为两输入端或非门的逻辑符号，逻辑函数表达式为

图8－12　两输入端或非门逻辑符号

或非门的真值表见表8－6。

表8－6　或非门的真值表

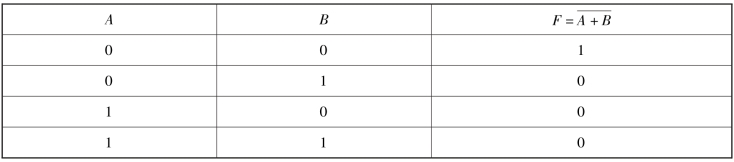
与非逻辑功能为：输入有1，输出为0；输入全0，输出为1。

3.异或门

“异或门”也称“异或逻辑”，它是两个变量的逻辑函数。图8－13所示为异或门逻辑符号，逻辑函数表达式为

异或门的真值表见表8－7。

图8－13　异或门逻辑符号

表8－7　异或门的真值表

异或逻辑功能为：输入相同，输出为0；输入不同，输出为1。

4.同或门

“异或”运算之后再进行“非”运算，则称为“同或”运算。实现“同或”运算的电路称为同或门。图8－14所示为同或门逻辑符号，逻辑函数表达式为

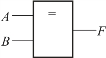
图8－14　同或门逻辑符号

同或门的真值表见表8－8。

表8－8　同或门的真值表

(www.xing528.com)

异或逻辑功能为：输入相同，输出为1；输入不同，输出为0。

1.2.3　布尔代数与逻辑函数化简

1.布尔代数的基本公式

在布尔逻辑代数运算中，可运用一些定律，现将有关定律总结如下。

1）基本运算

2）交换律

3）分配律

4）结合律

5）重叠律

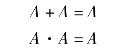
6）吸收律

7）还原律

8）冗余律

9）摩根定理

2.逻辑函数的代数法化简

逻辑函数的化简就是使逻辑函数式最简，以便设计出最简的逻辑电路，从而节省元器件、优化生产工艺、降低成本和提高系统可靠性。

1）并项法

运用基本公式，将两乘积项合并成一项，并消去一个变量。

例如：

2）吸收法

运用基本公式，消去多余的项。

例如：

3）消去法

运用吸收律，消去多余因子。

例如：

4）配项法

运用基本运算，进行配项，然后再化简。

例如：

边学边练

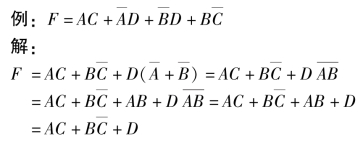
3.卡诺图化简

卡诺图是一种化简逻辑函数表达式的方法，如果仅仅使用基本定律和法则，复杂的表达式仍是不好化简的，而卡诺图可以帮助我们简化复杂表达式，从而以最小的逻辑门实现系统功能。

1）逻辑函数的卡诺图表示

（1）相邻最小项的概念。

相邻最小项：有逻辑相邻和几何相邻。

逻辑相邻：若两个最小项只有一个变量为互反变量，其余变量均相同，则这样的两个最小项为逻辑相邻，例如，最小项ABC和就是相邻最小项。

几何相邻：几何相邻的情况如下。

相接——紧挨着；

相对——任意一行或一列的两头（即循环相邻性，也称滚转相邻性）。

（2）用卡诺图表示最小项。

最小项的卡诺图：将n个变量的2n个最小项用2n个小方格表示，并且使相邻最小项在几何位置上也相邻且循环相邻，这样排列得到的方格图称为n变量最小项卡诺图，简称为变量卡诺图。

（3）卡诺图的结构。

二变量、三变量、四变量的卡诺图如图8－15所示。其中“1”表示原变量；“0”表示反变量，“mi”表示最小项。

图8－15　卡诺图结构

（4）用卡诺图表示逻辑函数。

由于卡诺图与真值表一一对应，即真值表的某一行对应着卡诺图的某一小方格。因此如果真值表中的某一行函数值为“1”，卡诺图中对应的小方格填“1”；如果真值表中的某一行函数值为“0”，卡诺图中对应的小方格填“0”，即可以得到逻辑函数的卡诺图。

边学边练

例：某逻辑函数的真值表如下，用卡诺图表示该逻辑函数。

解：该函数为三变量，先画出三变量卡诺图，然后根据真值表将8个最小项F的取值0或者1填入卡诺图中对应的8个小方格中即可。

例：用卡诺图表示逻辑函数。

解：写成简化形式：F＝m0＋m3＋m6＋m7，然后填入卡诺图：

2）逻辑函数的卡诺图化简法

卡诺图化简逻辑函数的原理是具有相邻性的最小项可以合并，并消去不同的因子，合并的结果为这些项的公因子。

用卡诺图化简逻辑函数的步骤如下：

（1）把给定的逻辑函数表达式填到卡诺图中。

（2）找出可以合并的最小项（画圈，一个圈代表一个乘积项）。

（3）写出合并后的乘积项，并写成“与－或”表达式。

化简依据：

（1）2个相邻的最小项结合，2项可以合并为1项，并消去1个不同的变量。

（2）4个相邻的最小项结合，4项可以合并为1项，并消去2个不同的变量。

（3）8个相邻的最小项结合，8项可以合并为1项，并消去3个不同的变量。

总之，2n个相邻的最小项结合，2n项可以合并为1项，并消去n个不同的变量。

边学边练

例：利用卡诺图化简。

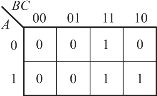
解：

最终，化简表达式为

F＝AB＋BC

例：用卡诺图化简逻辑代数式

解：首先通过逻辑表达式画卡诺图

最终，化简表达式为：F＝AB＋BC。

画圈的原则如下：

（1）圈的个数尽可能减少（因一个圈代表一个乘积项）。

（2）圈尽可能大（因圈越大可消去的变量越多，相应的乘积就越简）。

（3）每画一个圈至少包括一个新的“1”格，否则是多余的，所有的“1”都要被圈到。