常见数制编码：BCD码8421、5421、2421等

1.1.1　几个基本概念

1.数码

数码是能表示物理量大小的数字符号。例如，日常生活中十进制数使用的是0、1、2、3、4、5、6、7、8、9十个不同数码。

2.数制

计数制的简称，表示多位数码中每一位的构成方法，以及从低位到高位的进制规则。常用的有十进制、二进制、八进制和十六进制等。

3.权

每种数制中，数码位于不同位置，它所代表的位置的含义是不同的。各数位上数码表示的数量等于该数码与相应数位的权之乘积。例如：十进制数123中，“1”表示1×102，“2”表示2×101，“3”表示3×100。

1.1.2　十进制、二进制、八进制、十六进制数的表示方法

1.十进制数

十进制数是人们在日常生活中最熟悉的一种数制，它由0、1、2、3、4、5、6、7、8、9十个数码构成，按“逢十进一”“借一当十”的原则计数，10是它的基数。任一个十进制数都可以用加权系数展开式来表示，n位整数十进制数用加权系数展开式表示，可写为

（N）10＝an－1an－2…a1a0＝an－1×10n－1＋an－2×10n－2＋…＋a1×101＋a0×100

式中，（N）10的下标10表示十进制数。

例如：（185）10＝1×102＋8×101＋5×100

其中，10称为基数，即所用数码的数目；102、101、100称为该位的权，它是根据各个数码在数中的位置得到的，且都是基数10的整数次幂。

2.二进制数

二进制数中只有0和1两个数码，按“逢二进一”“借一当二”的原则计数，2是它的基数，二进制数的各数位的权为2的幂。

例如：

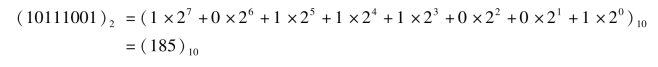
3.八进制数

八进制数由0、1、2、3、4、5、6、7八个数码构成，按“逢八进一”“借一当八”的原则计数，8是它的基数，各数位的权为8的幂。

例如：（123）8＝（1×82＋2×81＋3×80）10＝（83）10

4.十六进制数

十六进制数由0～9、A、B、C、D、E、F十六个数码构成，分别对应十进制的0～15，按“逢十六进一”“借一当十六”的原则计数，16是它的基数，各数位的权为16的幂。

例如：（3EC）16＝（3×162＋14×161＋12×160）10＝（1004）10

1.1.3　数制转换

1.非十进制数转换为十进制数

非十进制数转换为十进制数，就是把非十进制数转换为等值的十进制数。只需将非十进制数按权展开，然后各项相加，就得到相应的十进制数。

边学边练

例：将二进制数（10011）2转换成十进制数。(www.xing528.com)

解：（10011）2＝（1×24＋0×23＋0×22＋1×21＋1×20）10＝（19）10

例：将十六进制数（5A7）16转换成十进制数。

解：（5A7）16＝5×162＋A×161＋7×160＝（1447）10

例：将八进制数（126）8转换成十进制数。

解：（126）8＝1×82＋2×81＋6×80＝（86）10

2.十进制数转换为非十进制数

把十进制数转换为非十进制数，需要把十进制数的整数部分和小数部分分别进行转换，然后再将整数部分和小数部分的转换结果合并起来。

整数部分：（基数除法）十进制数的整数部分转换为非十进制数可以采用“连除法”，用欲转换的非十进制数的基数连续除该数，直到除得的商为0为止，每次除法所得余数作为非十进制数转换结果的系数，并取最后一位余数为最高位，依次按从下往上顺序排列。

小数部分：（基数乘法）十进制数的小数部分转化成二（八、十六）进制小数可以采用“乘二取整法”（“乘八取整法”“乘十六取整法”），即用2（8、16）去乘欲转换的十进制小数取其整数部分作为转换结果的系数，直到纯小数部分为0或到一定精度为止。每次乘法得到的整数作为转换结果的系数，最先得到的整数作为高位，后得到的整数作为低位，按从上往下的顺序依次排列。

整数部分的转换概括为“除2、8、16取余，余数倒序排列”；小数部分的转换概括为“乘2、8、16取整，整数顺序排列”。

边学边练

例：（38）10＝（　）2＝（　）8＝（　）16

解：

读写顺序自下而上：100110，所以：

（38）10＝（100110）2

同理：

所以：（38）10＝（46）8＝（26）16。

3.二进制数与八进制、十六进制数之间的转换

二进制数转换成八进制数，只需要把二进制数从低位到高位，每3位分成一组，高位不足3位时补0，写出相应的八进制数，就可以得到与二进制数对应的八进制转换值。反之，将八进制数中每一位都写成相应3位二进制数，所得到的就是与八进制对应的二进制转换值。

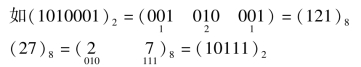
同理，二进制数转换成十六进制数，只需要把二进制数从低位到高位，每4位分成一组，高位不足4位时补0，写出相应的十六进制数，所得到的就是与二进制数对应的十六进制转换值。反之，将十六进制数中的每一位都写成相应的4位二进制数，便可得到十六进制数对应的二进制转换值。

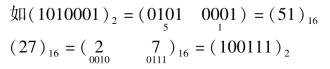
1.1.4　编码

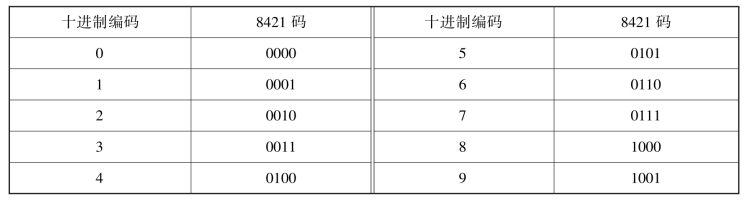
编码就是用数字或某种文字和符号来表示某一对象或信号的过程，十进制编码或某种文字和符号的编码难于用电路来实现，在数字电路中一般采用二进制数。用二进制表示十进制的编码称为二－十进制编码，又称BCD码。常见BCD码有8421码、5421码、2421码等编码方式。以8421码为例，8421分别代表对应二进制的权，即当哪一位二进制为1时，所代表的十进制为相应的权。十进制对应的8421码见表8－1。

表8－1　十进制对应的8421码