3.3.1 电容定义

1.11 电容的种类

1.12 电容充电放电
在电容器的两个极板间加上电源后,极板上分别积聚起等量的异性电荷,在介质中建立起电场,同时储存电场能量。电源移去后,电荷仍然聚集在极板上,电场继续存在。所以,电容器是一种能够储存电场能量的实际器件。电容元件就是实际电容器的理想化模型,其图
电容器的品种和规格有很多,如图1-34所示。就其构成原理来说,电容器都是由两块金属极板隔以不同的绝缘物质(如云母、绝缘纸、电解质等)组成的。所以任何两个彼此靠近而且又相互绝缘的导体都可以构成电容器。这两个导体叫作电容器的极板,它们之间的绝缘物质叫作介质。形符号如图1-35所示。

图1-34 常用的电容器

1.13 电容容量标识方法
图1-35中+q和-q为该元件正、负极板上的电荷量。若规定其电压的参考方向由正极板指向负极板,则任何时刻正极板上的电荷量q与其两端的电压U有以下关系:
![]()
![]()
图1-35 电容元件的图形符号
式中,C称为电容元件的电容,它是用来衡量电容元件容纳电荷本领的一个物理量,是一个与电荷q、电压U无关的正实数。
电容的单位为法拉(F),常用单位还有微法(μF)和皮法(pF),其换算关系为
1F=106μF=1012pF
为了叙述方便,我们把电容元件简称为电容,所以“电容”这个术语及它的符号C,一方面表示一个电容元件,另一方面也表示这个元件的参数。
3.3.2 电容的连接
1.电容的串联
图1-36所示为三个电容的串联电路。
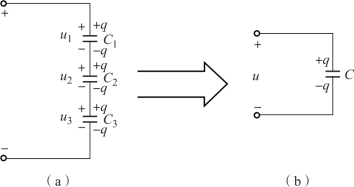
图1-36 电容的串联电路
(a)串联电路;(b)等效电路
电压u加在电容组合体两端的两块极板上,使这两块与外电路相连的极板分别充有等量的异性电荷q,中间的各个极板由于静电感应而产生感应电荷,感应电荷量与两端极板上的电荷量相等,均为q,如图1-36(a)所示。因此电容串联时,各电容所带的电量相等,即
q=C1u1=C2u2=C3u3
串联电路的总电压为
![]()
由图1-36(b)可知等效电容所带的总电量也为q,其电压与电量的关系为
![]()
综上所述,等效条件为

即电容串联时,其等效电容的倒数等于各串联电容的倒数之和。
各电容的电压之比为
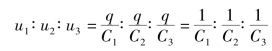
即电容串联时,各电容两端的电压与其电容量成反比。
![]() (https://www.xing528.com)
(https://www.xing528.com)
从电容串联的性质可以看出,电容器串联后总的电容量减小,整体的耐压值升高。如果标称电压低于外加电压,可以采用电容串联的方法,但要注意,电容器串联后一方面电容变小;另一方面,电容器的电压与电容量成反比,电容量小的承受的电压高,要考虑标称电压是否大于电容器的耐压值。
2.电容的并联
图1-37所示为三个电容的并联电路。
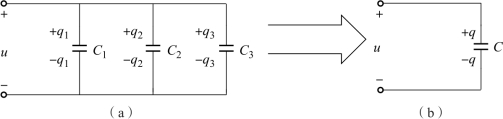
图1-37 电容的并联电路
(a)并联电路;(b)等效电路
C1、C2、C3上加的是相同的电压u,它们各自的电量为
q1=C1u;q2=C2u;q3=C3u
所以
q1∶q2∶q3=C1∶C2∶C3
即电容并联时,各电容所带的电量与各电容器的电容量成正比。
电容并联后所带的总电量为
q=q1+q2+q3=C1u+C2u+C3u=u(C1+C2+C3)
由图1-37(b)可知等效电容为
![]()
即电容并联时,其等效电容等于并联的各电容器的电容量之和。
![]()
从电容并联的性质可以看出,当电路所需电容较大时,可以选用电容量适合的几个电容器并联。电容器并联时加在各电容器上的电压相同,所以电容器并联使用时,为了使各个电容器都能安全工作,所选择的电容器的最低耐压值不得低于电路的最高工作电压。
边学边练
例:如图1-38所示,已知C1=C4=10μF,C2=C3=20μF,求
(1)当开关S打开时,ab间的等效电容Cab;
(2)当开关S闭合时,ab间的等效电容Cab。
解:(1)当S打开时,C1与C2串联,C3与C4串联,两串联电路再并联,所以
![]()
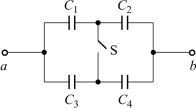
图1-38 电路
得
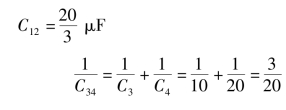
得
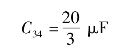
因此
![]()
(2)当S闭合时,C1与C3并联,C2与C4并联,两并联电路再串联,所以
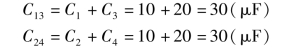
因此
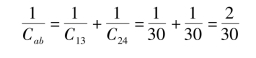
得
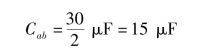
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




