3.1.1 电阻定义

1.5 电阻
电路中自由电子的移动不是畅通无阻的,电源、负载和导线都具有不同程度上阻碍电流流动的性质,这种固有性质称为电阻,即物体阻止电流通过的本领称为电阻。在电路图中,常用理想电阻元件来表示电阻对电流的这种阻碍作用,用字母R表示,如图1-18所示。
![]()
图1-18 电阻元件
电阻的单位是欧姆(Ω),常用单位还有千欧(kΩ)、兆欧(MΩ)等,它们之间的换算关系为
1MΩ=103kΩ=106Ω
任何导体都有电阻,电阻的大小与它本身的物理条件有关。实验证明:导体的温度变化时,它的电阻值也随之变化。一般的金属材料导体在温度升高后,电阻值会增大。导体的电阻值与温度成正比。
在温度不变时导体的电阻跟它的长度L和导体的电阻率ρ成正比,跟它的横截面积S成反比,这就是电阻定律,即
![]()
电阻率的大小是由导体的材料决定的,表1-1所示为一些材料在20℃时的电阻率。
表1-1 电阻率20℃

导体电阻率越接近10-8Ω·m,导电性越好,常用的导体材料是铜和铝;绝缘体电阻率大于10-8Ω·m,用它隔离电流不会有显著的漏电,如塑料、橡胶等;半导体电阻率在10-5~107Ω·m,用它可以制造晶体管,如硅、锗材料。
3.1.2 欧姆定律

1.6 欧姆定律
1826年德国科学家欧姆通过实验证实:“流过导体中的电流与导体两端的电压成正比,与导体的电阻成反比。”这就是欧姆定律。欧姆定律是反映电路中电压、电流、电阻等内在关系的一个极为重要的定律,也是电工技术中一个最基本的定律,用公式表示为

3.1.3 常用电阻(器)在欧姆定律中,若![]() 是常数,即电阻值不随电压、电流的变化而变化,则称为“线性电阻”。线性电阻的电压电流关系曲线(即伏安特性曲线)为一条通过坐标原点的直线,如图1-19(a)所示。如果电阻值随电压、电流的变化而改变,则称为“非线性电阻”,如半导体二极管,其伏安特性曲线为一条曲线,如图1-19(b)所示。
是常数,即电阻值不随电压、电流的变化而变化,则称为“线性电阻”。线性电阻的电压电流关系曲线(即伏安特性曲线)为一条通过坐标原点的直线,如图1-19(a)所示。如果电阻值随电压、电流的变化而改变,则称为“非线性电阻”,如半导体二极管,其伏安特性曲线为一条曲线,如图1-19(b)所示。
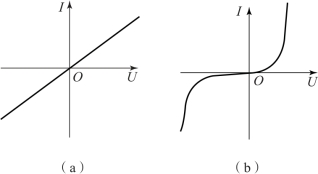
图1-19 电阻的伏安特性曲线
(a)线性电阻;(b)非线性电阻
线性电阻在电路中的应用非常广泛,在实际电路中,像白炽灯、电阻炉和电烙铁等,均可看成是线性电阻元件。本书讨论的电阻是线性电阻,在不加特殊说明时,所说的电阻均指线性电阻。
线性电阻又分为固定电阻和可变电阻。固定电阻的电阻值是定值,阻值不能变化。可变电阻是电阻值可以变化的,常称为电位器。
常用电阻器如图1-20所示。
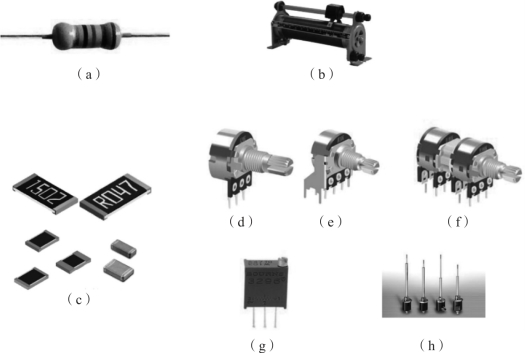
图1-20 常用电阻器
(a)色环电阻;(b)滑线变阻器;(c)表面贴装电阻;(d)单联电位器;(e)双联电位器;(f)四联电位器;(g)可调电阻;(h)推杆电位器
当电阻元件上的电压与电流方向一致时,元件吸收的功率为P=UI,由欧姆定律可推导出![]() ,说明电阻元件是耗能元件。电路中大多数电气设备都具有消耗电能的电磁性能,它们吸收功率,引起电气设备发热。
,说明电阻元件是耗能元件。电路中大多数电气设备都具有消耗电能的电磁性能,它们吸收功率,引起电气设备发热。
电阻器的主要性能参数包括标称电阻值、允许偏差、额定功率等。电阻器的标称电阻值和偏差一般都直接标注在电阻上,常用的标注方法主要有直标法和色标法。直标法是将电阻的主要参数直接标注在电阻表面上,色标法是将电阻的主要参数用颜色(色环)标注在电阻表面上。
图1-21所示为电阻的色标法。电阻的色环通常为4道,其中3道距离较近,作为阻值标注,另一道距离较远,作为误差标注。第一道、第二道各表示一位有效数字,第三道表示零的个数,第四道表示允许误差。
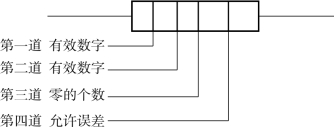
图1-21 电阻的色标法

1.7 色环电阻读取
色环颜色与表示的数码对照如表1-2所示,色环颜色与误差对照如表1-3所示。
表1-2 色环颜色与表示的数码对照

表1-3 色环颜色与误差对照

边学边练
例:已知一色环电阻颜色标注如图1-22所示,请读出该电阻阻值和误差。
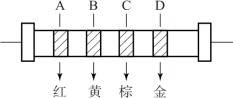
图1-22 色环电阻颜色标注
解:色环A—红色;B—黄色;C—棕色;D—金色。
该电阻的阻值为24×101±5%,即240±5%Ω。
3.1.4 电阻的测量
电阻的静态值常常使用万用表来测量。测量电阻时,红表笔插入“VΩ”,黑表笔插入“COM插孔”,转动功能量程选择开关至电阻挡“Ω”,数字万用表即构成欧姆表。电阻的测量如图1-23所示,将两表笔(不分正、负)分别接被测电阻两端金属部位,测量中可以用手接触电阻,但不要把手同时接触电阻两端,这样会影响测量精确度(人体是电阻很大的导体),LCD显示屏即显示出被测电阻R的阻值。测量大阻值电阻时,LCD显示屏的读数需要几秒钟后才能稳定,这是正常现象。
3.1.5 电阻的连接

1.8 万用表测电阻
1.电阻的串联
把电阻一个一个地按首尾顺序连接起来的连接方式称为电阻的串联,如图1-24所示。
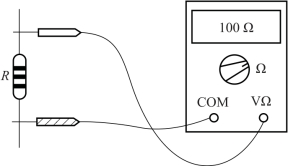
图1-23 电阻的测量
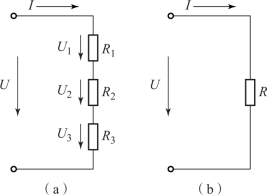
图1-24 电阻的串联
(a)电路图;(b)等效图
电阻串联电路的主要特点如下:
(1)电路中电流处处相等,即
![]()
(2)串联电路两端的总电压等于各个电阻两端的电压之和,即
![]()
(3)串联电路的等效电阻(即总电阻)等于各串联电阻之和,由
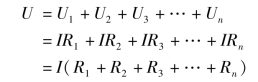
![]()
得(4)串联电路具有分压作用,电压分配与电阻成正比,由
![]()
得
![]()
各电阻的分电压与总电压的关系为(https://www.xing528.com)
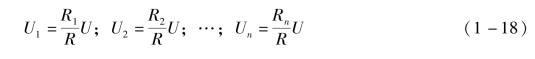
边学边练
例:有一盏额定电压为40V、额定电流为5A的弧光灯要接入220V电路中,问应串联一只阻值和功率为多大的电阻分压?
解:弧光灯的额定电压为40V,要接入220V电路中,所串联的分压电阻两端的电压为
UR=U-U1=220-40=180(V)
串联电路电流处处相等,故电阻通过的电流也是5A,由
![]()
电阻的功率为
P=URI=180×5=900(W)
2.电阻的并联
把电阻并列地接在电路中两个共同端点之间的连接方式称为电阻的并联,如图1-25所示。
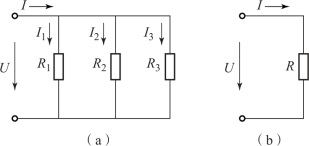
图1-25 电阻的并联
(a)电路图;(b)等效图
电阻并联电路的主要特点如下:
(1)并联电阻两端电压相等,即
![]()
(2)并联电路总电流等于各个电阻上的电流之和,即
![]()
(3)并联电路等效电阻(即总电阻)的倒数等于各个电阻倒数之和,由
I=I1+I2+I3+…+In
得
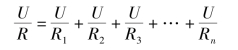
故
![]()
如果两个电阻并联,则它们的总电阻为
![]()
如果有n个相同的电阻Rn并联,则总电阻为
![]()
即并联电路中,总电阻总是小于每个分电阻。
(4)并联电路具有分流作用,电流分配与电阻成反比,由
![]()
得
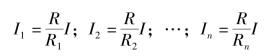
可见电阻越大,其分得的电流越小;电阻越小,其分得的电流越大。
利用这一关系,可求出各分支电流。常用的是两个支路的电流分配公式,由两个电阻并联的特点,可得

边学边练
例:如图1-26所示,有两盏220V/40W的照明灯并联接在电源上,求流过灯泡的电流、总电流和总电阻。
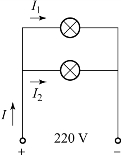
图1-26 照明灯电路
解:流过照明灯的电流
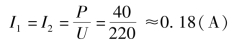
两盏照明灯为并联,总电流为
![]()
照明灯电阻为
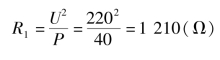
两盏照明灯并联总电阻为
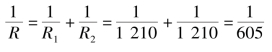
即
R=605Ω
3.电阻的混联
在实际应用中,使用更多的是电阻的混联电路,即在同一个电路中,既有电阻的串联,又有电阻的并联,如图1-27所示。
对于电阻混联电路的计算,只要按电阻的串联和并联的计算方法,一步一步地把电路化简,最后就可以求出总的等效电阻了。判别混联电路的串、并联关系应掌握以下三种方法。
(1)看电路的结构特点。
若两电阻首尾相接就是串联,若首首、尾尾相接就是并联,图1-27中R2与R3首首、尾尾相接,是并联;而R4与R5是首尾相接,是串联。
(2)看电流、电压关系。
若流经两个电阻的电流相同,就是串联;若两个电阻承受同一个电压,就是并联。图1-27中R2与R3承受相同的电压,是并联;而R4与R5流过相同的电流,是串联。
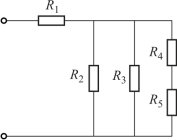
图1-27 电阻混联电路
(3)对电路做变形等效。
对电路结构进行分析,选出电路的节点,以节点为基准将电路结构变形,然后进行判别。电路等效变换示意图如图1-28所示。
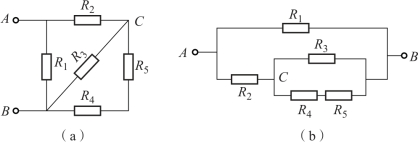
图1-28 电路等效变换示意图
(a)混联电路;(b)等效电路
边学边练
例:如图1-29所示电路,求Rab。
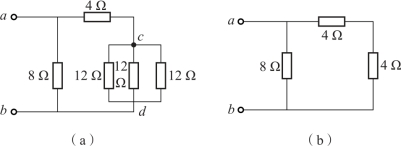
图1-29 电路
(a)电路图;(b)等效电路
解:由图1-29可知,8Ω电阻直接连接到a和b两点,而4Ω和3个12Ω的电阻,要经过3个12Ω的电阻并联,然后再与4Ω相串。将图1-29(a)所示电路等效成图1-29(b)所示电路,其等效电阻为
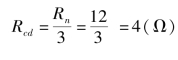
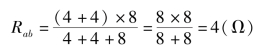
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




