分析残余压应力变化与裂纹扩展驱动力影响的算例分析

在这一部分内容里，将通过一个算例来分析残余压应力的变化、连接显微硬度与屈服强度的约束因子的变化和激光硬化层的弹性模量与涂层弹性模量比值的变化对裂纹扩展驱动力的影响。为了研究这些因素对裂纹扩展驱动力的影响，始终假定裂纹的初始长度是一定的。同时，假定激光热处理硬化区中心的显微硬度沿着硬化层深度方向的变化规律遵循一个指数函数的变化规律：

这里的D0和δ为待定常数。从图7.6可得到：

当x＝h1，H＝Hm＝D0；当x＝h1＋h2，H＝H0＝D0exp（δh2）。

因此，只要知道这两点的显微硬度值就可以确定常数D0和δ。对于一种特殊的情形，取文献［70］的一个实验结果，该实验结果有：

当x＝h1，H≈8×109Pa；当x＝h1＋h2，H≈3×109Pa。

激光淬火层的总深度h2≈0.6 mm。于是由式（7.21），可以确定常数D0和δ，其相应的显微硬度变化规律可以由式（7.22）给出：

一些用来计算J、JH和Jtot的参数由表7.1给出。

表7.1　一些用来计算J、JH和Jtot的参数

值得强调的是，表7.1中的所有参数在下面的所有计算过程中均保持不变。(www.xing528.com)

在第一个算例里，令残余压应力σR＝200 MPa，约束因子k＝1／2.5［53］，涂层的弹性模量E1＝290 GPa（铬层的弹性模量），淬火钢基体的弹性模量E2＝210 GPa。给定这些已知条件后，可求得总的裂纹扩展驱动力Jtot＝1.351 4×103（J／m2）。值得强调的是，该值将作为下面计算分析中的规整化因子。

首先，研究残余压应力对裂纹扩展驱动力的影响。在这部分工作中，将残余压应力无量纲化，应力归整化因子为σ0＝Fp/［B（a－h1）］（Fp、B、a、h1均为常数），约束因子k＝1／2.5，涂层的弹性模量E1＝290 GPa，淬火钢基体的弹性模量E2＝210 GPa。令表示不同残余压应力下的裂纹扩展总驱动力，将与归整化因子Jtot无量纲化后，根据给定的这些已知条件，可以描绘出随σR/σ0的变化规律，如图7.11所示。

图7.11　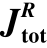/Jtot随σR/σ0的变化规律，σ0=Fp/［B（a-h1）］

其次，研究约束因子k的变化对总裂纹扩展驱动力的影响。为方便起见，定义另一无量纲系数k′，且k′＝1/k。基于文献［49－55］的研究成果，无量纲系数k′可在1.7～3.0之间变化，在这一计算中，残余压应力σR＝200 MPa，涂层的弹性模量E1＝290 GPa，淬火钢基体的弹性模量E2＝210 GPa。令表示不同约束因子下的裂纹扩展总驱动力，将与归整化因子Jtot无量纲化后，根据给定的这些已知条件，可以描绘出随约束因子k′的变化规律，如图7.12所示。

最后，研究激光硬化层的弹性模量E2与涂层弹性模量E1的比值E2/E1的变化对裂纹扩展驱动力的影响。在这一部分计算中，令残余压应力σR＝200 MPa，约束因子k＝1／2.5，涂层的弹性模量E1＝290 GPa。令表示不同模量比值E2/E1下的裂纹扩展总驱动力，将与归整化因子Jtot无量纲化后，根据给定的这些已知条件，可以得到随模量比值E2/E1的变化规律，如图7.13所示。

图7.12　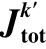/Jtot随约束因子k′（k′=1/k）的变化规律

图7.13　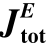/Jtot随模量比值E2/E1的变化规律