压入法对韧性涂层/脆性基体材料界面结合性能影响的研究

在科研实践与工程实际中，压入法（indentation test）［84－106］也是一种十分普遍的定量、半定量或定性的测量界面结合性能的方法。它具有操作方便、试样制备简单等优点。压入方法有多种，按压头的位置分，常见的有涂层表面压入法（coating surface indentation method）、侧面基体压入法（cross－sectional indentation method）和界面压入法（interfacial indentation method）。在压入法中，压头的形状也有多种，常见的有球形压头、圆锥形压头、三棱锥压头、四棱锥压头、楔形压头等。

（1）涂层表面压入法。涂层表面压入法［84－94］是将压头直接压在涂层的表面，其示意图如图1.19所示。采用涂层表面压入法测量界面结合强度是建立在实验的基础上，在能判断界面瞬时开裂的条件下，利用瞬时开裂所对应的载荷，即临界载荷，建立有限元模型，根据压入过程中得到的应力应变关系，采用合适的有限元接触单元，计算临界载荷情形下的界面应力场。

Qi等［87］采用涂层表面压入法得出了求解金刚石薄膜与金属基体（多晶铜）界面结合强度的表达式

式中，E为金刚石薄膜的弹性模量；x为界面上点的横坐标；a为常数，取决于压入载荷的大小、压头的形状和涂层与基体材料的性质以及涂层的厚度；b也是一个常数，主要取决于涂层与基体材料的性质以及涂层的厚度。

另一种计算界面剪切强度和拉伸强度的模型为采用球形压头的赫兹接触模型，根据临界压痕半径，涂层和基体材料的几何、力学等参数，可以求得界面的结合强度。由于公式较长，在此未列出，详细计算公式可参阅文献［85，107］。

这种方法适合于弱结合界面，且必须配备有能判断界面是否开裂的设备，如光学显微镜、声发射等。这种方法的不足之处是在实验的过程中，表面压入很容易使脆性涂层产生众多的径向裂纹和环向裂纹，如果有限元的模型与实验过程中的真实情况差别很大，计算出来的界面结合强度就会存在着很大的误差。

（2）侧面基体压入法。侧面基体压入法［95－101］是把压头放在试件侧面离界面一定距离的基体上，其示意图如图1.20所示。

图1.19　涂层表面压入法示意图

图1.20　侧面基体压入法示意图

近几年来，这种方法被用来测量涂层与基体材料的界面结合性能（也包括界面的韧性指标［98－101］）。Zhang等［96－97］采用此方法测量了热喷涂类涂层与韧性基体的界面结合强度，如图1.21所示。

这种方法的新颖之处是利用了侧向力（图1.20中的Fx）与压入时间曲线的斜率突变来判断界面是否开裂。这种得出界面结合强度的方法采用了有限元与Jakl S I和Rammerstorfer FG［108］提出的二次脱层准则（quadratic delamination criterion）来计算和判断当界面开裂瞬时在界面上产生的最大正应力和最大剪应力，这最大的正应力和剪应力分别就是界面的拉伸强度和剪切强度。二次脱层准则常用于复合材料的脱层分析［109－111］，其表达式为

图1.21　侧面基体压入法研究Al2O3/Al6061的界面结合强度［97］

式中，σxz、σyz为界面的剪应力；σzz为界面的正应力；ZS、ZN为界面的剪切强度和拉伸强度。满足式（1.24）的界面剪应力、正应力即为界面的剪切强度和拉伸强度。由于方程中有两个未知数，如果要计算出界面的剪切强度和拉伸强度，至少要在不同位置完成两次压入实验。同时还得采用计算程序来判断界面上满足式（1.24）的应力点，排除那些不满足式（1.24）的应力点。

由于这种方法的特点是压头不直接压涂层，而是压在离界面一定距离的基体上，这样就可以避免涂层直接接触载荷而使问题复杂化。这种方法非常适合于弱结合界面的脆性涂层／脆性基体材料，因为脆性基体材料在压入的过程中可以不考虑基体材料的塑性变形，这样就可以使问题相对变得简单些。同时，侧面基体压入法也适合于具有弱结合类的Ⅰ类、Ⅳ类涂层体系。

侧面基体压入法除了被用来研究界面结合的强度指标外，还被用来研究界面结合的韧性指标。Sánchez等［98］在靠近脆性涂层的脆性基体上做压入实验，脆性基体材料的边缘剥离效应使压头外侧基体从整个基体材料上剥落，随着载荷的继续施加产生的侧推力将剥落下来的基体向外推，从而造成涂层和整体基体之间的拉应力，并最终导致界面破坏。建立的压入模型如图1.22所示。

非常巧妙的是，他们采用薄板理论推导出了求解界面断裂韧性的解析表达式为

式中，λ＝a/b，a和b的尺寸如图1.23所示；D为薄板的弯曲刚度；E为薄膜的弹性模量；ν为薄膜的泊松比，且有

图1.22　建立的压入模型［98］

图1.23　侧面基体压入法导致的结果示意图［98］

对于侧面基体压入法，除了国外的Sánchez等［98］做了一些研究外，国内的研究者Zheng等［99－100］在他们研究的基础上，将侧面基体压入法推广到脆性的压电薄膜上，采用各向异性板理论研究了BaTiO3、CoFe2O4和PZT－4薄膜的界面结合性能。另外，Elizalde等［101］还将侧面基体压入法用于研究电镀铜韧性涂层／Si脆性基体材料的界面结合性能，材料横截面的SEM（扫描电镜）图和材料与压痕位置的示意图如图1.24所示，侧面基体压入法导致的电镀Cu／SiO2基体材料的SEM图如图1.25所示。

图1.24　材料横截面的SEM图和材料与压痕位置的示意图

（a）材料横截面的SEM图；（b）材料与压痕位置的示意图［101］

图1.25　侧面基体压入法导致的电镀Cu/SiO2基体材料的SEM图［101］

对于韧性涂层／脆性基体材料，Elizalde等［101］采用了有限元计算的方法求解体系的界面结合性能，其计算公式为(www.xing528.com)

式中，GCi为界面临界能量释放率；ΔUe为Cu薄膜在压入过程中所发生的弹性变形；ΔUp为Cu薄膜在压入过程中所发生的塑性变形；ΔA为Cu薄膜开裂的裂纹面面积。

（3）界面压入法。界面压入法［102－106］是一种将压头直接压在界面上，从而使界面开裂的方法。其示意图如图1.26所示。

Démarécaux，Chicot和Lesage等［102－106］提出了一个叫“外观上的界面断裂韧性”（apparent interface toughness）的概念，其表达式为

图1.26　界面压入法示意图

其中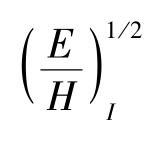被定义为

式中，E为弹性模量；H为硬度；下标I、S和C分别代表界面、基体和涂层。这一“外观上的界面断裂韧性”的优越之处在于分别考虑了涂层与基体的力学性能，不足之处在于该方法适合于较厚的涂层，对于较薄的涂层不太适合，因为对于太薄的涂层，不易使压头的中心位置正好控制在界面上。

在压入法测量界面结合强度时，至少含有以下两点不足：其一，在压头的附近应力状态非常复杂，产生的边缘效应使得难以精确地计算出实际应力的大小，从现有的成果看，研究者们都是采用在压头的附近划分足够精细的网格密度来弥补这一不足。其二，当测量对象为脆性涂层时，有时界面还未开裂，而涂层本身就先开裂了。如果出现这种情形，将给采用有限元计算界面结合性能带来理论建模的复杂性，如在建模时得考虑涂层动态三维裂纹的扩展模型，计算出涂层裂纹在动态扩展过程中引起的界面应力场的变化和界面瞬时开裂时界面上对应的应力状态。前面的研究成果都是针对只出现界面开裂而没有出现涂层开裂的情形。在采用侧面基体压入法测量电镀铬层／钢基体材料的界面结合性能时，发现在界面开裂前，涂层先出现3条十分明显的裂纹，其中一条先出现在正对压痕中心的位置上，且裂纹方向近乎垂直于界面，后出现的两条是对称于前一条裂纹的斜裂纹（与界面有一定的夹角），如图1.27所示。

这种情形的出现至少取决于这几个因素，即压头的形状、压头中心离界面的距离、加载的速率、涂层与基体材料的弹塑性性能和界面结合性能的强弱。其中有一很重要的因素就是界面结合性能越强，涂层就越容易先开裂［112－113］。这其中的大部分因素对界面开裂影响的理论与实验研究尚未见报道。对于由界面结合性能强导致的界面还未开裂而涂层先开裂的情形，压入法也可以从定性的角度去评价该种材料体系的界面结合性能，如给定压入点的位置、压头形状、载荷大小等参数，去比较产生的界面裂纹的长度［98］。

图1.27　侧面基体压入法测量电铬镀层/钢基体材料的界面结合性能时产生的开裂情形

总之，压入法针对不同的涂层体系，可以从定量、半定量或定性的角度去评价界面结合性能。对于界面结合性能较弱的Ⅰ类、Ⅲ类、Ⅳ类涂层体系，压入法还是可以从定量的角度去评价界面结合性能的，而对于界面结合性能较强的Ⅰ类、Ⅲ类、Ⅳ类涂层体系，界面结合性能不容易得出，压入法也可以从定性的角度去评价界面结合性能。

上面讨论了压入法测量涂层与基体间的界面结合性能，下面讨论采用压入法测量涂层的断裂韧性。在采用压入法研究涂层的断裂韧性时，Holleck和Schulz［114］提出可通过在压入载荷大小相同的情形下，去比较涂层的裂纹长度来确定涂层的断裂韧性；Kustas等［115］提出通过比较涂层的剥落直径来比较涂层的断裂韧性，这些都是非常定性的方法。在定量的研究方法中，Lawn等［116］提出了一个计算断裂韧性的公式

式中，FP为压入载荷的大小；E和H分别为涂层的弹性模量和硬度；C为径向裂纹的长度，如图1.28所示；δ为一个经验常数，对于标准的维氏金刚石棱锥和立方压头，δ通常分别取0.016［117］和0.0319［118］。另外一些研究者［119－121］提出压入载荷FP、E、H、C和涂层的断裂韧性KIC有如下关系：

式中，σ为涂层表面的残余应力；对于Berkovich金刚石压头，χr＝0.016（E/H）1／2。

图1.28　维氏压头导致的涂层表面SEM开裂［116］

其实，采用压入法测量涂层的断裂韧性，最可靠的还是采用能量法［122－127］。能量法的原理是涂层发生了开裂和没有发生开裂的能量差值被认为涂层的能量释放量，这一能量差值可以从载荷与位移曲线图上得到。一旦涂层的能量释放率已经确定，就可以通过式（1.7）得到涂层的断裂韧性。Li等［122－123］指出，硬质薄膜在可控的压入载荷作用下其断裂特征可以简化为三个阶段，如图1.29所示。

图1.29　硬质薄膜在压入载荷作用下开裂的三个阶段［122］

第一阶段：由于在压头的附近会产生很大的应力场而产生第一个环向裂纹，此裂纹通常贯穿涂层的整个厚度。

第二阶段：由于产生的侧向应力而导致的界面开裂、失稳和剥落。

第三阶段：第二个贯穿涂层厚度的环向裂纹产生，由于产生的弯曲应力使得失稳的涂层剥落。

第一个环向裂纹和第二个环向裂纹所产生的能量释放量可以通过相应的载荷－位移曲线的变化来计算，如图1.30所示。

在图1.30中，OACD为加载曲线，DE为卸载曲线，那么ABC的面积就代表了产生的第一个环向裂纹和第二个环向裂纹之间的能量差值，这一能量差值代表了产生的涂层环向裂纹所释放的能量，其具体表达式为［122］

式中，E为涂层的弹性模量；νf为涂层的泊松比；2πCR为涂层平面上的裂纹长度；t为涂层的厚度；ΔU为涂层裂纹开裂前后的能量差值。

图1.30　压入载荷作用下载荷-位移曲线发生的跳跃与相应的能量释放量之间的关系［122］