如何提高土壤敷设的热阻性能？

若无特殊要求，一般地下敷设时可取标准深度1m，并可近似地认为电缆表面、土壤表面均为等温面。土壤为均匀媒质，其热阻系数为kρ′_T4，一般k≈2/3，则kρ_T′₄=ρ_T4。电缆散发到土壤的热流均流向大地表面，如图1-4-7所示。

根据电工学中的镜像法原理，若电缆敷设深度为L，以集中参数W代替流向土地表面的分布热流，则和W相对称在土地表面上部L处，假设有一个-W为其虚像。那么，+W和-W之间的热场和实际热场相同。接下来，可采用电轴法求场中的温度，如图1-4-8所示。

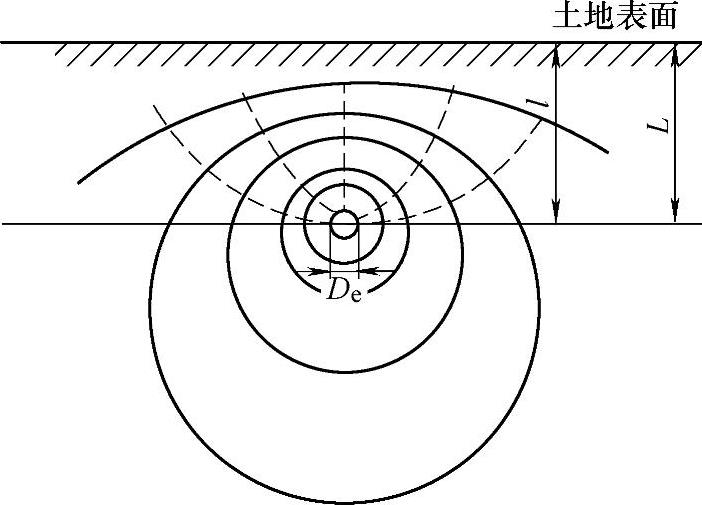
图1-4-7 敷设在土壤中的电缆热流场

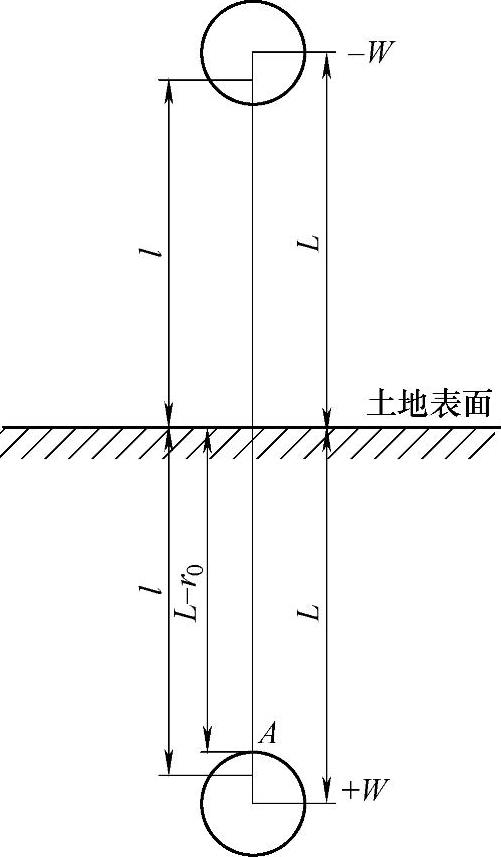
图1-4-8 用镜像法计算土地热阻说明

电缆的截面积较大，电缆发热不集中在几何中心，而可认为集中在电缆的某处。热流集中处称为等效热轴。设土地表面的温度为参考温度，电缆半径为r_e，等效热轴到参考点的距离为l，电缆几何中心到参考点的距离为L，故电缆表面A点到负热轴的距离为l+（L-r_e）；A点到正热轴的距离为l-（L-r_e），则A点的温度为

故土壤的热阻为

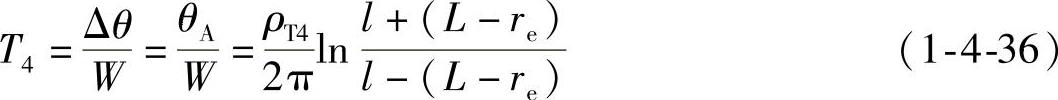
又因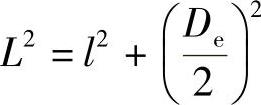则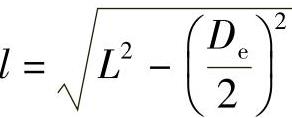，将其代入式（1-4-36）得

一般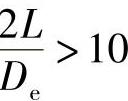时，有

如果有多根电缆敷设于土地中，必然相互有热的影响，相当于增加了热源，可按镜像原理求取。如图1-4-9所示为负载电流相同的n根电缆组成的电缆群，其中如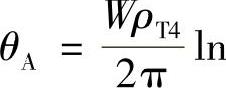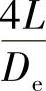，则

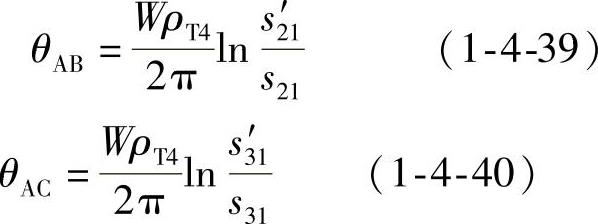
故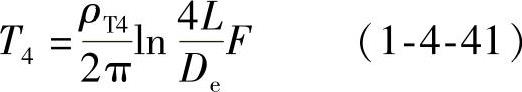

式中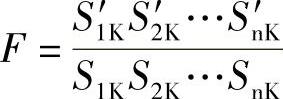，，S_1K、S_2K，…，S_nK为电缆1，2，…，n中心至电缆K中心距离；S_1K′，S_2K′，…，S_nK′为电缆1，2，…，n的镜像中心至电缆K中心的距离。

对于敷设在地下水泥槽管道中的电缆，T₄为T₄′、T₄″、T‴₄三者之和，如图1-4-10所示。

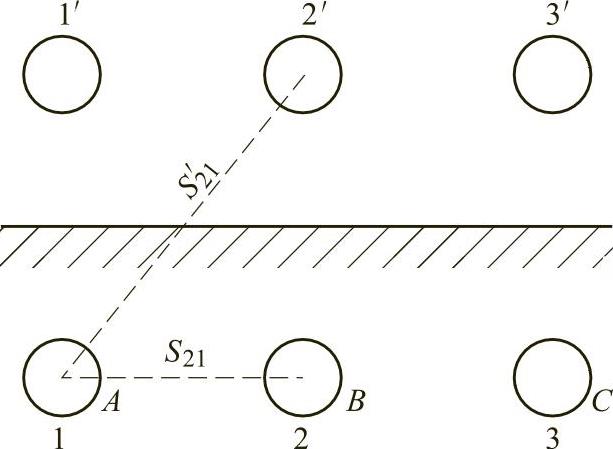
图1-4-9 多根电缆镜像法求热阻示意图

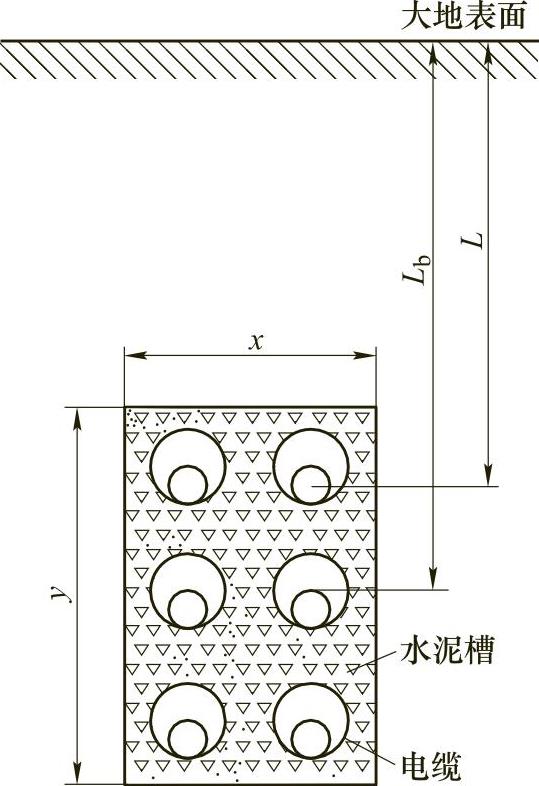
图1-4-10 敷设在地下水泥槽中电缆示意图(www.xing528.com)

T₄′为电缆表面到管道内壁的热阻，可按下式求取

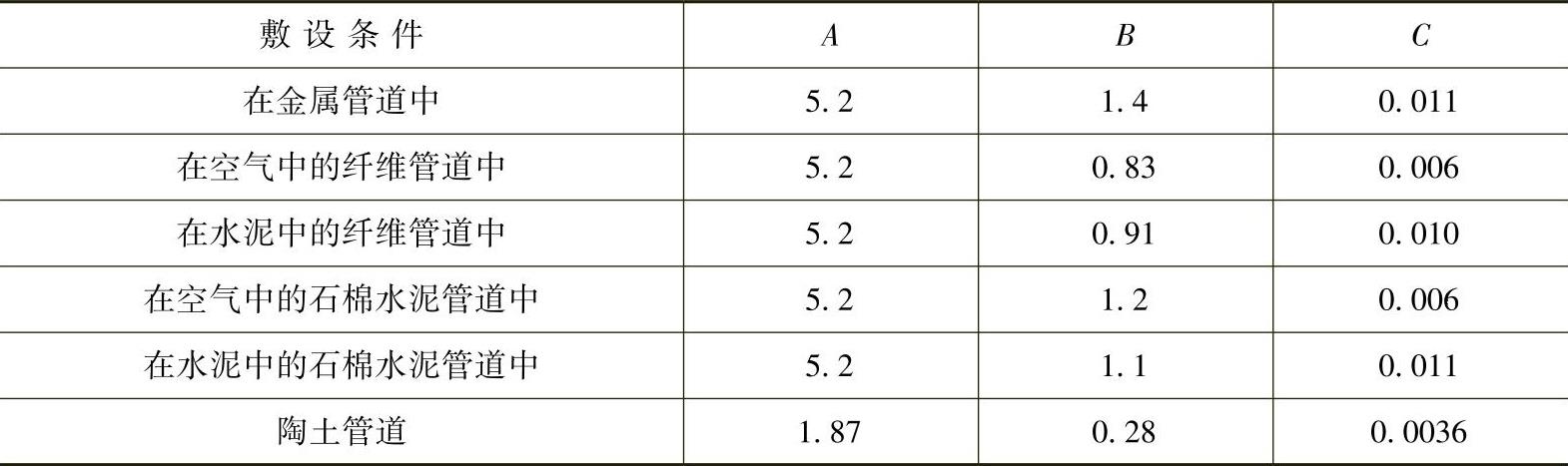
式中，θ_m为电缆和管道间填充介质的平均温度。先用假定值，如50℃，如果需要而后用校正值反复进行计算；D_e为电缆外径；A、B、C为与电缆有关的常数，其值列于表1-4-4中。

表1-4-4 常数A、B、C的数值

T₄″为管道本身热阻，可近似认为管道内外表面均为等温面，可按圆柱形公式计算，即

式中，p″_T4为管道材料的热阻系数；D₀为管道外径；D_d为管道内径。

T‴₄为管道外部热阻。首先假设管道周围媒质全部为水泥，故可按式（1-4-42）计算，只不过热阻系数为水泥热阻系数ρ_c，故

式中，F为热邻近效应因数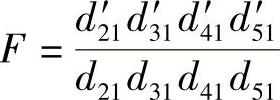，，d₂₁′，d₃₁′，d₄₁′，d₅₁′和d₂₁，d₃₁，d₄₁，d₅₁分别为第一根电缆到第2、3、4、5根电缆的虚像和实际的距离。

实际上，周围媒质为水泥槽和土壤，故应从式（1-4-44）中减去水泥槽外的假设水泥部分，加上实为土地的部分。

为此可把长方形的水泥槽等效成圆形槽，其等效半径r_b可根据经验公式求出，则有

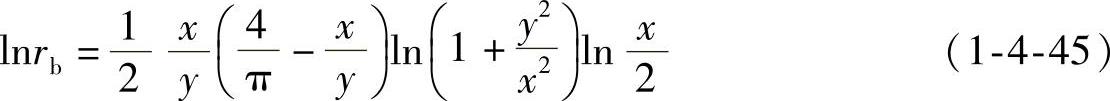
式中，x、y分别为水泥槽端面短边和长边的长度，不考虑其位置。

若水泥槽有n根管道，水泥槽中心到地面的距离为L_b，则假设槽外水泥的热阻为

而实际槽外为土壤的热阻为

故T‴₄应为

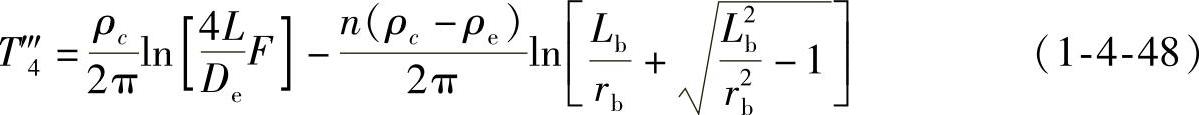
式中，ρ_c为土壤的热阻系数。