电缆热路方程及温度允许范围考虑全面损耗与层级因素

若求解热场方程，运算较为复杂。在实际工程中，可将热场问题转化为热路问题，以求出载流量的计算公式。这样可大大简化运算，也符合电缆实际运行情况。

以一单芯电缆为例。为了方便起见，可先考虑导电线芯损耗。设导电线芯半径为r_c，绝缘外半径为R。首先求出稳态时绝缘层中的温度分布公式。为此可将式（1-4-6）改写为

对其进行两次积分得

θ=C₁lnr+C₂ （1-4-8）

C₁、C₂为积分常数，可根据初始条件求取。

当r=r_c时，θ=θ_c（线芯温度）。故有

θ_c=C₁lnr_c+C₂ （1-4-9）

又因在稳态情况下，线芯产生的热流可认为全部进入绝缘层，则据富氏定律：

又对式（1-4-8）两边求导

据式（1-4-10）、式（1-4-11）两式可得

将式（1-4-12）代入式（1-4-9）得

将C₁、C₂均带入式（1-4-8）可得

式（1-4-14）即为稳态时绝缘层中任一点的温度分布公式。

当r=R时，θ=θ_s（金属屏蔽层温度），由式（1-4-14）可得

令为热阻系数，故式（1-4-15）可写成

又令为热阻，故式（1-4-16）可写成

θ_c^-θs=W_cT₁ （1-4-17）

图1-4-3 热路图

即由线芯损耗在导电线芯至金属屏蔽层间产生的温升等于热流和热阻之积。写成热路图如图1-4-3所示。这样就将热流场问题转化为热路问题。

以上分析仅考虑了导电线芯损耗，现再单独考虑由介质损耗产生的温升，也即相当于电缆加电压U₀后开路的情况。此时线芯损耗W_c=0，绝缘层单位体积发出的热流W_i=γE²。由式（1-4-5）得

将其改写成为(www.xing528.com)

式中，λ为导热系数；γ为绝缘层等值电导率；r_c为导电线芯半径；R为绝缘层外半径；U₀为相电压；r为绝缘层中任意一点到电缆中心的距离。

对式（1-4-19）两边积分可得

两边除以r再积分

积分常数C₁、C₂可利用初始条件求取。

当r=r_c时，θ=θ_c；又根据富氏定律，有

故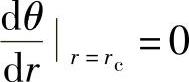，将其代入式（1-4-20）中，则

同理将r=r_c，θ=θ_c及C₁代入式（1-4-21）中得

将C₁、C₂代入式（1-4-21）中，经整理可得：

式（1-4-25）考虑介质损耗时绝缘层中任意一点的温度分布方程，即

式中，为介质总的损耗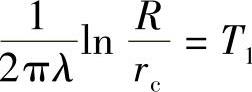；为绝缘层热阻。故当r=R，θ=θ_s时式（1-4-21）可写为

即由于介质损耗在绝缘层两端产生的温升，等于介质损耗和绝缘层热阻乘积的1/2。这可理解为介质损耗为分布参数，流经整个绝缘层的介质损耗所产生的热流，实际可等效地看成为总的介质损耗热流的1/2。

同理，若将导电线芯损耗W_c、介质损耗W_i、金属屏蔽层损耗W_s和铠装层损耗W_p同时考虑，令绝缘层热阻为T₁，内衬层热阻为T₂，外护层热阻为T₃，周围媒质热阻为T₄，则根据叠加原理，其热路方程为

式中，θ_c为导体允许最高温度，见表1-4-1；θ_a为周围媒质温度，见表1-4-2。电缆全部等效热路图如图1-4-4所示。

表1-4-1 各种形式的电缆允许最高工作温度

表1-4-2 周围媒质温度 （单位：℃）

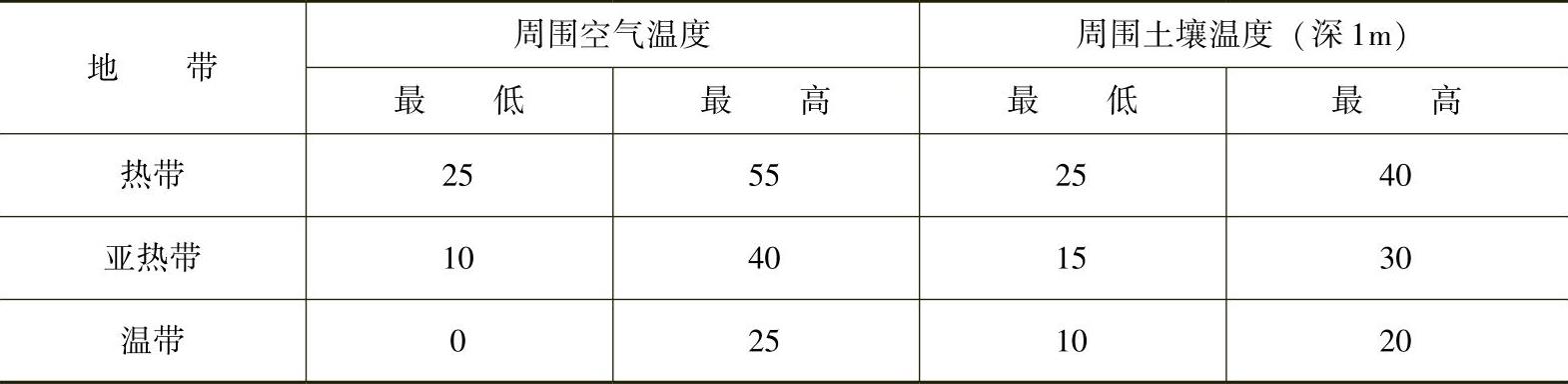
图1-4-4 电缆全部等效热路图