真空介质中放电现象的试验研究与分析

根据高压工程关于气体放电现象的电子碰撞理论，在一定的场强作用下，影响电极间气体放电的形成主要有气体分子的密度ρ和自由电子运动的平均行程λ两个因素。即当气体的密度大时，自由电子在电场中向阳极运动的加速过程中与其他分子的碰撞次数增多，λ很短，能量不易积聚，使产生导致击穿的电子崩的概率小。如使电极间气体击穿，必须升高外施电压，以便电子在电场中获得更多的动能产生电子崩。相反，气体密度小，自由电子在运动中碰撞次数少，λ长，能量容易积聚，增大了出现电子崩的概率，因而在外施电压较低时气体即可击穿。试验发现，如固定电极的间距、改变气体的压力，在（1～2000）×1.33×102Pa范围内，气体放电电压随气压的升高而增大、随气压的降低而减小，然而进一步抽取密封容器内的空气，降低气压，在达到1.33×（10-3～10-6）Pa的真空状态后，电极间的放电电压反而逐渐升高，这是因为此时空气密度极低，能够产生电子崩的自由电子所需的平均行程必须非常大，才可集聚足够的动能碰撞其他气体分子产生电子崩引起击穿。以上现象完全可以用电子碰撞理论来解释。

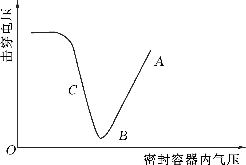
图1-1　密闭容器内气体击穿电压与气压的关系曲线

如果继续抽气，容器内压力更低，即达到某一更高的真空度后，电极间的击穿电压不再增高而呈现一种类似饱和的状态。定性地描述这一过程的曲线如图1-1所示。图中，A—B和C点以下曲线部分的气体放电规律可用巴申（Paschen）定律定量地加以描述和计算。对应以气体压力p和电极间距d的乘积pd为变量，放电电压U的数学表达式如下

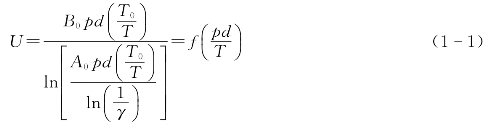
式中：A0、B0为标准温度（20℃）时与气体种类和温度有关的常数；γ为与电极材料和表面状态有关的系数；p为气体压力；d为电极间距；T0、T为标准状态的温度与试验时的温度。(www.xing528.com)

在温度一定时，式（1-1）可写成U=f（pd）的形式。

按式（1-1）绘制的计算曲线如图1-2所示，它是一个有着极小值的V形曲线。计算时空气的常数取值A0=0.11/（cm·Pa），B0=2.74V/（cm·Pa），γ=0.025（铜电极）。极小值的右侧对应于图1-1中曲线的A—B区段，显示了放电电压随气压的升高而增大；在极小值的左侧，对应图1-1中曲线的B—C的区段，表明放电电压随气压降低而增大的特性。图1-2中还同时绘出了在均匀电场中电极间放电电压U与pd关系试验实测的曲线。除pd值很低的一段曲线外，其余基本与巴申定律的计算值一致。

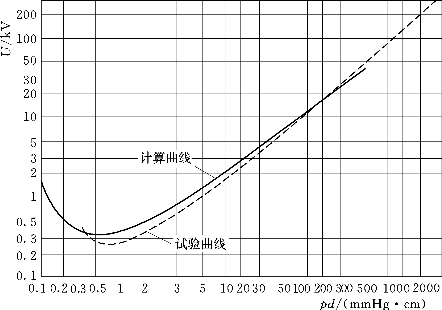
图1-2　均匀电场中电极间放电电压U=f（pd）的试验曲线和计算曲线

根据电子碰撞理论，在1.33×10-1Pa的真空中，自由电子能够产生使电极间击穿的电子崩所需的平均自由行程λ=26m；在1.33×10-3Pa的真空中，λ必须增大到26km。应注意到的一个现象是：在真空灭弧室中，电极的间距（断口）通常仅有几毫米到二十几毫米，远远小于λ的值，应该不会发生击穿，但事实表明在外施电压作用下却具有一定的击穿电压，因而高真空状态下产生放电的原因以及击穿电压饱和现象都无法用电子碰撞理论解释，它们应该有着另外不同的放电机理，然而至今人们仍未发现其真正的原因。