宏宏复合微纳运动系统低速性能仿真研究

1.宏宏复合微纳运动系统摩擦参数辨识

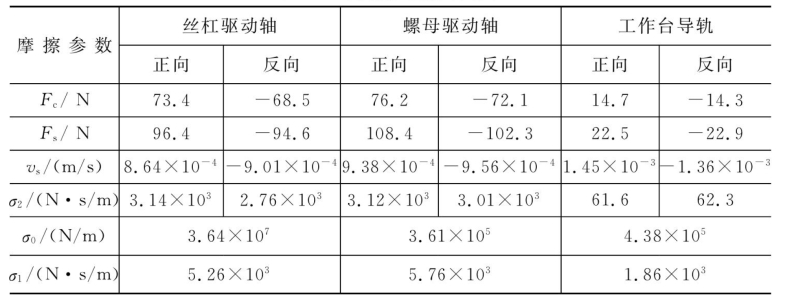
在对单自由度宏宏复合微纳运动系统进行摩擦建模分析的基础上，按照遗传算法进行了摩擦参数辨识，辨识结果如表7-3所示。表中：Fc为滑动导轨处的库伦摩擦力，N；Fs为滑动导轨处的最大静摩擦力，N；vs为滑动导轨处的Stribeck速度，m/s；σ2为滑动导轨处的等效黏性摩擦系数，N·s/m；σ0为滑动导轨处的等效刚性系数，N/m；σ1为滑动导轨处的等效阻尼系数，N·s/m。比较发现，SDSS和NDSS两个宏动系统摩擦参数相近，实际进行宏宏复合微纳运动系统设计时也希望如此。

表7-3　摩擦参数辨识结果

如图7-5所示，当工作台低速运行时，速度低于vc就会产生爬行现象，vc称为临界速度。从图7-12所示的系统摩擦参数辨识特性曲线中可知，丝杠驱动轴的临界转速约为0.4 mm/s（等效到工作台的直线运动速度为2 mm/s），工作台的临界速度约为6.0 mm/s，即驱动轴临界速度要远低于工作台。

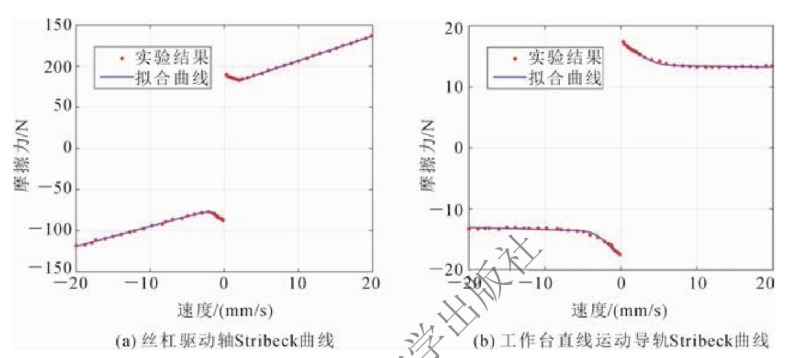
图7-12　系统摩擦参数辨识特性曲线

2.宏宏复合微纳运动系统低速性能仿真试验

宏宏复合微纳运动系统摩擦参数辨识结果如表7-3所示，仿真中位置输入均为斜坡输入，输入速度为匀速。宏宏复合微纳运动系统在丝杠单独驱动下，简称为SDSS单驱动运行模式，若在丝杠和螺母双驱动下，进行宏宏复合差动工作时，简称为SDSS-NDSS双驱动运行模式。

图7-13（a）～（l）分别为工作台在SDSS和SDSS-NDSS两种运行模式下，工作台的合成速度分别为1.65 mm/s、1.0 mm/s、0.5 mm/s、0.1 mm/s、10 mm/s，以及SDSS、NDSS不同宏动速度（v1、v2）合成下的仿真结果。图7-13（a）所示结果说明，在SDSS运行模式下，工作台直线进给速度为1.65 mm/s时发生了爬行现象。该速度值介于驱动轴与直线运动导轨的Stribeck速度之间，工作台以该速度进给时，丝杠与工作台同时处于预滑动摩擦区，受Stribeck效应的影响，工作台的速度响应出现了严重的振荡现象，将1.65 mm/s定为临界转速。(www.xing528.com)

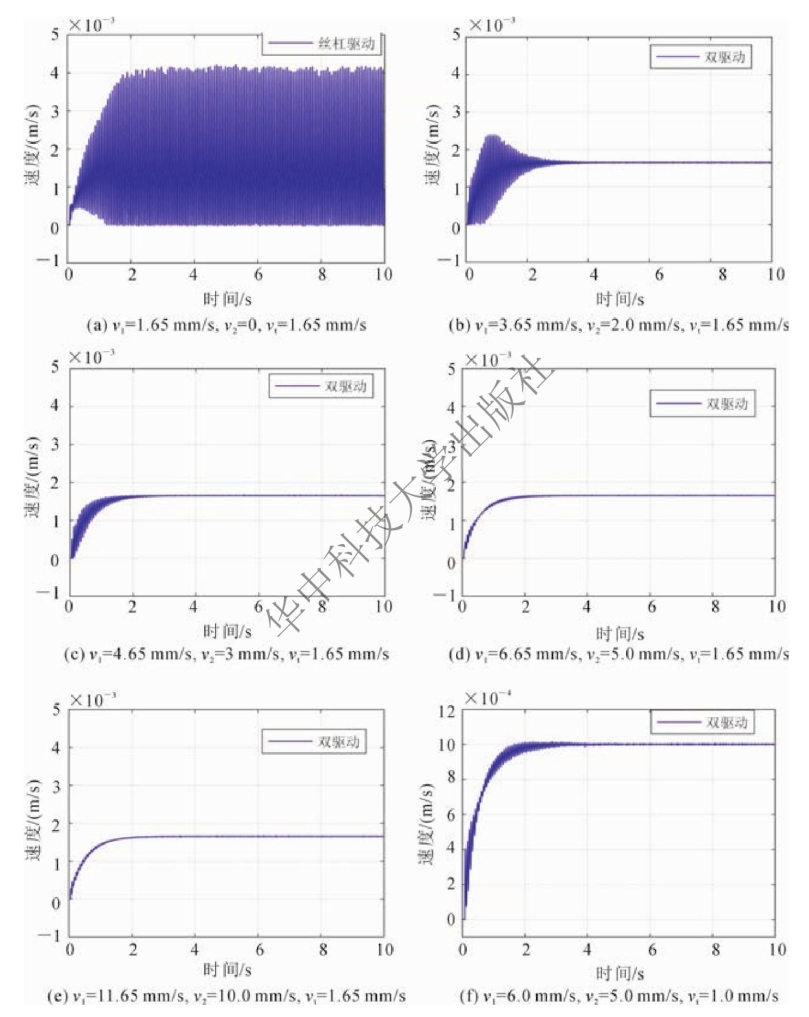
图7-13　不同工作模式下工作台的速度响应曲线

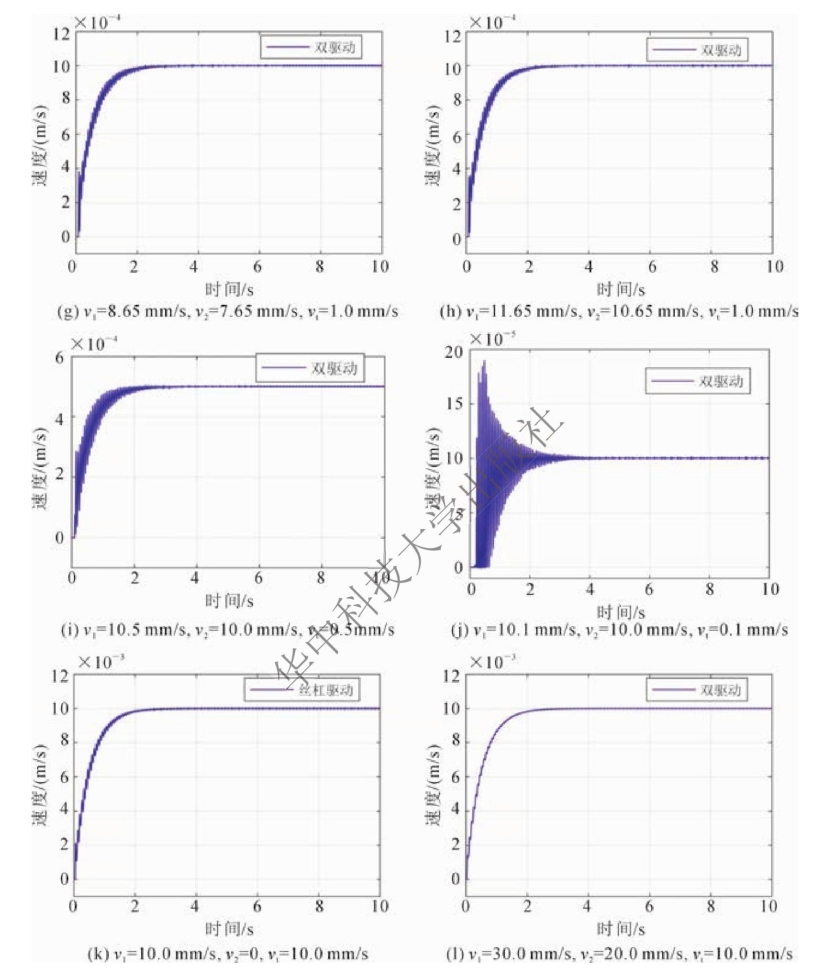
续图7-13

由图7-13（b）可以看出，当丝杠驱动轴转速高于临界转速，但螺母驱动轴转速略高于临界转速时，工作台的速度响应在开始阶段发生过渡振荡，调整时间达到4 s之后，速度响应趋于稳定。在图7-13（c）中，丝杠驱动轴转速与螺母驱动轴转速都高于临界转速，工作台速度只在初始阶段发生了很小的过渡振荡，调整时间为2.2 s。

图7-13（d）（e）给出了当两驱动轴转速均高于临界转速时，工作台速度的输出变化情况。对图7-13（c）～（e）进行对比发现，随着驱动轴转速升高，工作台在加速阶段的速度振荡逐渐减小。如图7-13（e）所示，在速度组合为v1=11.65 mm/s，v2=10 mm/s时，在工作台加速阶段几乎看不到明显的速度振荡。并且，当两轴转速均高于临界转速时，调整时间几乎不变。与图7-13（a）进行比较发现，在宏宏复合双驱动模式下，两驱动轴可以同时工作在相对高速区，即高于临界转速，成功避开了Stribeck效应的影响，克服了单驱动模式下，丝杠驱动轴在低速下不可避免地接近或进入非线性爬行区域的缺点。

图7-13（f）～（h）为宏宏复合差动模式下，合成后工作台速度为1.0 mm/s时的仿真结果，图7-13（f）和图7-13（g）的对比较明显，调整时间由4 s缩短到接近2 s。可以看出，增大驱动轴的转速可有效补偿由合成速度降低带来的非线性干扰。图7-13（g）和图7-13（h）没有明显区别，说明在宏宏复合差动模式下，驱动轴转速超过临界速度一定值，就可以达到减小摩擦非线性干扰的效果，而不需要工作在特别高的转速。

在保证两驱动轴高于临界速度的前提下，进一步降低宏宏复合差动模式下工作台的进给速度。图7-13（i）所示为工作台进给速度为0.5 mm/s时的速度响应曲线，虽然调整时间高于进给速度为1.0 mm/s时的，但最终仍然可以获得均匀稳定的速度响应。经过反复仿真试验，如图7-13（j）所示，宏宏复合差动模式下工作台的临界爬行速度接近0.1 mm/s，该速度值远小于丝杠单驱动时工作台临界爬行速度，甚至低于两驱动轴的Stribeck速度，进一步验证了宏宏复合差动模式可以使工作台获得精确稳定的极低速响应。

图7-13（k）和图7-13（l）所示为工作台速度为10.0 mm/s时的仿真结果。可以看出，工作台的进给速度高于临界速度时，宏宏双驱动模式和丝杠单驱动模式的速度波动与调整时间没有明显差别。

通过对比分析，可以看出，当两宏动转速超过临界转速，即工作在线性摩擦区时，宏宏复合差动运动系统表现出更好的低速微量进给特性，且响应速度快。