宏宏复合微纳运动系统的动力学模型优化

1.丝杠单驱动伺服系统动力学建模

在丝杠单驱动伺服系统（SDSS）中，丝杠电机通过联轴器直接驱动丝杠旋转，进而转换为工作台的直线运动，将丝杠电机、丝杠、轴承等旋转组件统称为丝杠驱动轴，进行等效处理后分析可得如图7-6所示的SDSS动力学几何模型。

图7-6　SDSS动力学几何模型

图7-6中：Ts是丝杠电机的输出扭矩；Tsd是作用在丝杠上的驱动力矩，Fsd是作用在工作台上的驱动力；Tsf是作用在丝杠驱动轴上的等效摩擦力矩；Ff1是作用在导轨滑块上的摩擦力；Js是丝杠驱动轴的等效转动惯量；θms是丝杠电机轴转角；θs是丝杠转角；xn1是丝杠单驱动时螺母组件的轴向位移；xt1是丝杠单驱动时工作台的轴向位移；Mt是工作台总质量。则SDSS的动力学模型可表示为

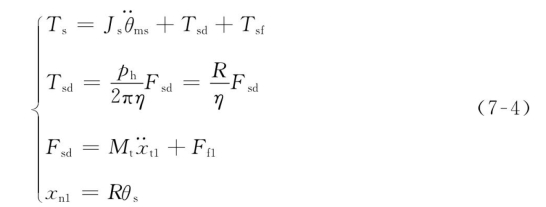
式中：ph——丝杠螺母的导程；

η——传动效率；

R——丝杠螺母传动比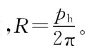

为了求出在丝杠单驱动时工作台实际的轴向位移量，需要综合考虑弹性部件的扭转变形和轴向伸长。用Kt1表示丝杠单驱动时系统的等效扭转刚度，有

式中：Kc——联轴器的扭转刚度；

Ksθ——丝杠的扭转刚度。

丝杠单驱动伺服系统的综合等效刚度为

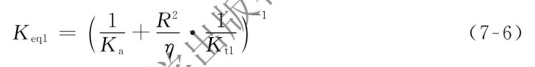
综合式（7-4）、式（7-6），SDSS工作台的轴向位移量为

2.螺母单驱动伺服系统动力学建模

在NDSS中，丝杠固定，将螺母电机、螺母、轴承、同步带轮等旋转组件统称为螺母驱动轴，经过等效处理分析后构建的NDSS动力学模型如图7-7所示。NDSS动力学模型可表示为

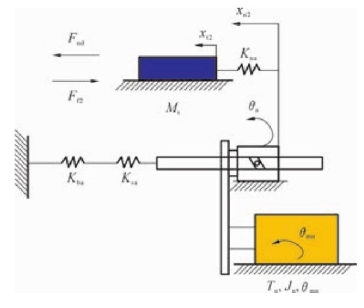
图7-7　NDSS动力学模型

式中：Tn——螺母电机的输出扭矩；

Jn——螺母驱动轴的等效转动惯量；

Tnd——作用在螺母上的驱动力矩；

Fnd——作用在工作台上的驱动力；

Tnf——螺母驱动轴处的等效摩擦力矩；

Ff2——直线导轨滑块处的摩擦力；

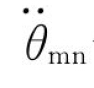——螺母电机轴转角加速度；

θn——螺母转角；

xn2——螺母单驱动时螺母组件的轴向运动加速度；

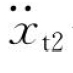——螺母单驱动时工作台的轴向运动加速度。

为了求出在螺母单驱动时工作台实际的轴向位移量，需要综合考虑弹性部件的扭转变形和轴向伸长。

用Kt2表示螺母和同步带的等效扭转刚度，有

(www.xing528.com)

式中：Knθ——螺母的扭转刚度；

KBθ——同步带的等效扭转刚度。

螺母驱动时，系统的等效轴向刚度Ka为

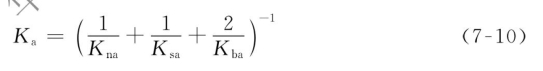
式中：Kna——螺母组件的轴向刚度；

Ksa——丝杠的轴向刚度；

Kba——轴承的轴向刚度。

根据以上得到的等效扭转刚度和等效轴向刚度，可计算出螺母单驱动伺服系统的综合等效刚度Keq2为

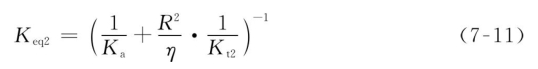
综合考虑系统的扭转变形和轴向伸长，可得到NDSS工作台实际轴向位移量的数学表达式，为

3.宏宏复合微纳运动系统动力学建模

综合SDSS和NDSS两个宏动系统动力学分析，不难得出宏宏复合微纳运动系统动力学模型，如图7-8所示。其中，Fd是复合驱动下工作台所受到的轴向驱动力；Ff是工作台导轨副摩擦力；xn是复合驱动下螺母组件的轴向位移；xt是复合驱动下工作台的轴向位移。

图7-8　宏宏复合微纳运动系统动力学模型

依据NDSS和SDSS动态匹配和便于控制原则，这里NDSS和SDSS两个宏动系统选用同型号伺服电机，且传动比参数一致、驱动轴转动惯量相等，即J=Jn=Js，故宏宏复合微纳运动系统动力学模型为

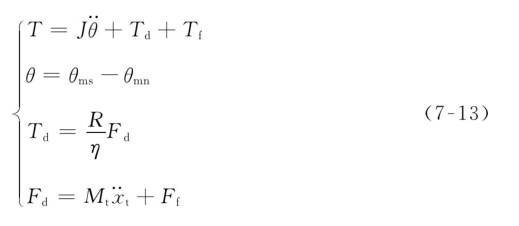
通过预先设计，可实现工作台在不同驱动方式下具有相同的运动参数，保证两单驱动和双轴差速微量进给伺服系统的综合刚度相等，即Keq=Keq1=Keq2，因此工作台在双伺服驱动工况下的位移为

4.交流伺服电机动力学建模

交流永磁式伺服电机具有硬的机械特性和较宽的调速范围，根据电磁学理论，其等效电路如图7-9所示。

图7-9　交流永磁式伺服电机在dq坐标系下的动态等效电路

交流伺服电机的动力学模型为

式中：idi，iqi——d轴、q轴的电流；

Ri——绕组等效电阻；

Ldi，Lqi——d轴、q轴电感；

ωei——转子角速度；

Ψi——转子磁场的等效磁链。则电磁转矩方程式可表示为

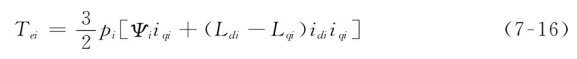
永磁同步电机转子为笼形，即Ldi=Lqi，采用id恒等于0的矢量控制方式，此时有

式（7-16）（7-17）中：Kti——转矩系数；

pi——极对数。