神经网络控制优化方案

基于人工神经网络的控制称为神经网络控制（neural network control，NNC），简称神经控制。

人工神经网络是从微观结构与功能上对人脑神经系统的模拟而建立起来的一类模型，具有模拟人的部分形象思维的能力，其特点是具有非线性特性、学习能力和自适应性。它是模拟人的智能的一种重要途径，在许多方面取得了广泛应用。神经网络的智能模拟用于控制，是实现智能控制的一种重要形式，近年来获得了迅速发展。

神经网络控制是指在控制系统中采用神经网络这一工具对难以精确描述的复杂的非线性对象进行建模，或充当控制器，或优化计算，或进行推理，或进行故障诊断等，亦即同时兼有上述某些功能的适应组合。从神经网络的基本模式看，主要有前馈型、反馈型、自组织型及随机型网络。目前，在控制领域内神经网络正在稳步发展，这种发展的动力主要来自三个方面：

第一个方面，处理越来越复杂的系统的需要；

第二个方面，实现越来越高的设计目标的需要；

第三个方面，在越来越不确定的情况下进行控制的需要。

因此，对于控制对象、环境与任务复杂的系统，可以采用人工神经网络智能控制的方法。目前常用的神经网络控制方法主要有BP（back propagation，反向传播）神经网络控制、RBF（radical basis function，径向基函数）神经网络控制等。

1.BP神经网络控制

BP神经网络是目前研究最为成熟、应用最为广泛的人工神经网络模型之一，如图4-4所示。由于具有结构简单、可操作性强、较好的自学习能力、可有效解决非线性目标函数的逼近问题等优点，因此它被广泛应用于自动控制、模式识别、图像识别、信号处理、预测、函数拟合、系统仿真等学科和领域中。但是，该模型的算法也存在许多不足。例如，初始学习率选取困难，收敛速度慢，接近最优解时易产生波动，有时还会出现振荡现象，对于具有增长趋势的时间序列预测问题外推效果不佳等。为了弥补这些缺陷，可通过整体变学习率的改进算法、基于神经网络的时间序列预测和优化新方法，来改善BP神经网络特性，构建基于BP神经网络的无约束和有约束优化问题的一般数学模型。此模型可用于PID控制器参数的优化整定。

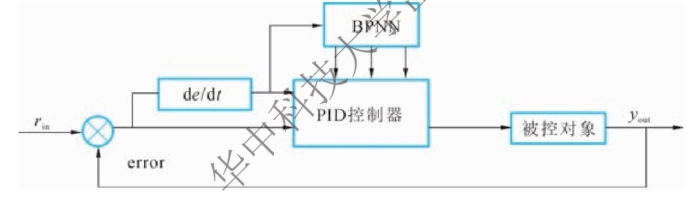
基于BP神经网络控制的PID控制器参数优化整定原理如图4-5所示。BP神经网络可以根据系统运行的状态，对PID控制器参数KP、TI、TD进行调节，使系统达到最优的控制状态。

2.RBF神经网络控制

在控制领域中，目前应用较多的网络是BP神经网络，但BP神经网络存在局部最优问题，并且训练速度慢、效率低。RBF神经网络在一定程度上克服了这些问题，因此它的研究与应用越来越得到重视。

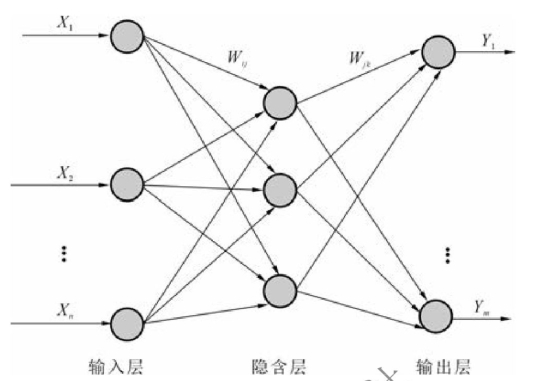
图4-4　BP神经网络结构

(www.xing528.com)

图4-5　BP神经网络控制对PID控制器进行参数优化整定的原理框图

1）RBF神经网络对非线性动态系统的建模

微纳运动实现系统的强非线性、蠕动、时变等特性，使得用常规算法对非线性系统建模难以获得理想效果，而RBF神经网络在这方面显示出其特有的优势，因此，近年来RBF神经网络较为广泛地用于非线性系统的建模、预测、分析等方面。RBF神经网络是一种典型的由输入层、隐含层、输出层组成的三层前馈式神经网络结构，如图4-6所示。

输入层为X=［x1，x2，…，xi，…，xn］，输入为转矩及给定转速与实际转速的差值。隐含层为H=［h1，h2，…，hj，…，hm］T，节点按高斯函数选取，由线性神经元组成。输出为所有隐含层节点的输出之和。

图4-6　RBF神经网络结构图

2）RBF神经网络与遗传算法

由于RBF神经网络的初始权值、阈值和高斯函数中心矢量不能较好地确定，而隐含层单元的传输函数又是不连续、不可微的，因此采用传统的优化方法可能陷入局部极小域。而遗传算法则具有不依赖这些信息的全局搜索特性，基于遗传算法优化的RBF神经网络，不仅可以获得网络的初始权值、阈值和高斯函数中心矢量的全局最优解，还可以提高神经网络的泛化性能，提升系统的精度、鲁棒性和自适应性，同时，在此基础上还可以和前馈控制、模糊系统、PID控制等结合，实现复合控制新策略。

3）RBF补偿复合控制策略

图4-7给出的是由前馈控制、PID反馈控制和径向基函数（RBF）补偿控制有机结合的一种三层复合控制方案。

其中，前馈控制规律设计简单，一般就是一种开环控制系统，利用输入或扰动信号的直接控制作用构成。

PID用作反馈控制项。在综合控制系统设计中，先进的最优控制理论用来调整PID控制增益，PID反馈控制器的设计可以使用线性二次型调节器（linear quadratic regulator，LQR）技术，来优化并稳健标称系统的性能。前馈加反馈结构通常也称为二自由度（2-DOF）控制。二自由度（2-DOF）控制可以满足许多实际控制要求，但是如果需要进一步提高性能，第三个控制组件可能会被启用。

图4-7　三层复合控制方案

径向基函数（RBF）补偿用于对非线性余项进行建模，在线性化闭环系统中用以匹配系统RBF的非线性部分，用来对未明确界定的非线性函数建模。径向基函数补偿为神经网络内的隐含层单元提供了一个基本函数集合，这些单元可扩大到更高维的隐含层单元空间。