在已知融合影像每个像元的光谱值r后,由于在融合过程中改变了各个波段的光谱值,因此这里选择本地纯净端元S:对于每一个融合影像中的像元,选取对应于原始影像中的8领域像元来列出方程,再采用最小二乘求解出结果。然后,利用线性光谱混合分析模型,通过模型反演可以求得高分辨率单个像元内各个端元组分的丰度。
考虑到融合后的结果是一幅空间范围扩大的高分辨率图像,因此,在融合影像中不同区域的端元光谱DN 值是不一样的。以南京地区SPOT5影像为例,图6-11表示为原始影像经过Gram-Schmidt光谱融合处理后的直方图对比情况。可以从各个波段的直方图统计中看出,融合前后的影像光谱有一个大面积的变化,因此,如果仍然把固定的纯净端元的光谱值应用到整幅影像上是不准确的。一般情况下,我们知道相邻像元应当更可能属于同一像元,所以选择不固定的本地纯净端元来对分别对每个区域进行分解会更加精确(Foody,1998;Schackelford和Davis,2003)。具体实现的步骤如下:
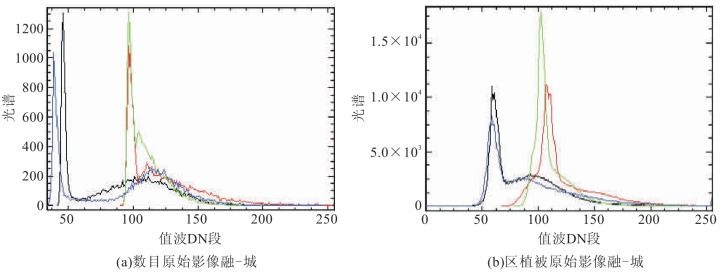
图6-11 融合前后影像直方图对比
选择融合影像中的像元R′,坐标是(m,n),对应于原始影像中的像元坐标(x,y),并且会满足(x=(int)m/f,y=(int)n/f),其中,f 为尺度大小。在融合影像中,对应8邻域的中心像元,同样可以列出类似的8个方程,那么对每一个波段及像元可以得到如下的方程:
![]()
即:
![]()
式中:![]() 为在第Bi 波段下坐标是(x,y)的光谱值;(https://www.xing528.com)
为在第Bi 波段下坐标是(x,y)的光谱值;(https://www.xing528.com)
![]() 为对应于每个纯净端元的组分比:
为对应于每个纯净端元的组分比:
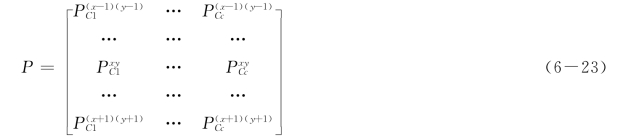
![]() 为在第Bi 波段下本地纯净端元光谱值,根据最小二乘法,可以得出对应的一个本地纯净端元光谱值为:
为在第Bi 波段下本地纯净端元光谱值,根据最小二乘法,可以得出对应的一个本地纯净端元光谱值为:
![]()
在求解过程中,为了强调对应像元(x,y)对纯净端元光谱的贡献,加入一个权重因子W,那么以上方程可以改为:
![]()
其中,

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




