超分辨率重建问题首先由Tsai和Huang提出,他们以傅立叶变换为基础框架,给出了一个利用多幅欠采样影像重建一幅高分辨率影像的频率域方法(Tsai,1984)。Kim 等(1993)对其方法进行了改进,进一步顾及了噪声和光学模糊的影响。此外,在频率域中也产生一些基于离散余弦变换(Rhee,1999)和小波变换(Nguyen and Milanfar,2000;Chan等,2003)的方法。然而,超分辨率重建技术在空间域得到了迅速的发展,产生了多种经典的超分辨率重建模型框架(沈焕锋,2007)。图6-6为高、低分辨率影像的简略像素坐标图,重建比率为1.5。
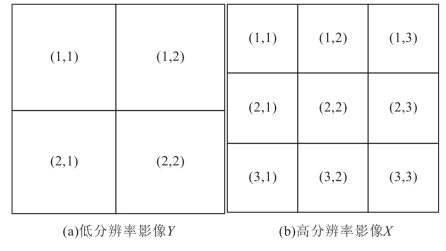
图6-6 低分辨率影像和高分辨率影像的像素坐标
如果将低分辨率影像的像素Y(1,1)投影到高分辨率影像的像素坐标中,它将覆盖高分辨率影像像素X(1,1)的全部,X(1,2)和X(2,1)的1/2及X(2,2)的1/4,由此可得如下方程:
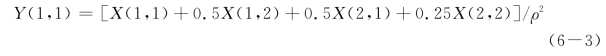
式中:Y(1,1)为低分辨率影像像素值;
X(1,1)、X(1,2)、X(2,1)、X(2,2)为高分辨率影像的像素值;
ρ为重建比率。
通过此方法,对每一个低分辨率影像的像素都可以建立一个观测方程,组成观测方程组。于是,观测模型的表达式可以写为:(https://www.xing528.com)
![]()
式中:y 为低分辨率影像像素矩阵;
x 为高分辨率影像像素矩阵;
A 为系数矩阵;
n为附加的噪声。
以上观测模型可以推广到亚像元定位方法中,把一幅经过重采样模糊化后的影像,当作一幅低分辨率影像,对影像进行混合像元分解,然后将每一个子图像进行超分辨率影像重建(图6-7)。这是一个简单的示意图,其中包含两种不同的端元组分,分别用黑色和白色圆圈来表示,图6-7(a)是原始的2×2像元栅格图,表示分解后的一幅分解丰度图像,其中每一个像元里面标明的数字代表端元组分在该像元中的百分比含量。图6-7(b)表示将原始像元分割成4×4的亚像元,使每一个亚像元的面积等于原始像元面积的1/16。图6-7(c)通过对同一位置的亚像元所占不同成分的百分比值进行比较,计算出原始像元中亚像元的个数,以对亚像元定位。例如,图中占端元比例25%的像元,可以求解出每一个亚像元的值(这里用×符号来表示),最后,在亚像元分布图中定位出4个亚像元(黑色圆圈)来代表这一种端元类型,而其他的12个亚像元(白色圆圈)代表其他的端元类型。所以,定义图6-7中(a)为低分辨率影像,(b)为高分辨率影像,建立观测模型,重建比率ρ=4,低分辨率影像每一个像元包含高分辨率影像的16个亚像元,由此建立方程组。
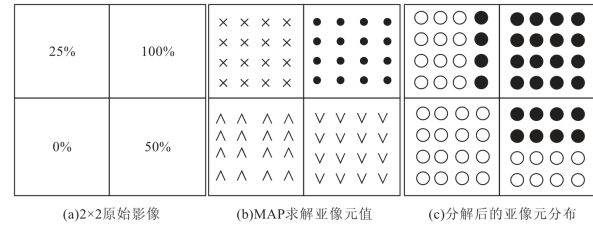
图6-7 亚像元定位模型示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




