【摘要】：研究表明，当满足亚像元间的空间依存度最大时，也可以把亚像元的定位看作是一种简单的线性最优化问题。由于目标函数和限制条件都是线性方程，所以把寻找方程的解变成线性最优化问题。当前，寻找线性最优解有各种各样的方法，以下引入一种新的理论模型，解决线性最优解的问题。
研究表明，当满足亚像元间的空间依存度（空间相关或空间自相关）最大时，也可以把亚像元的定位看作是一种简单的线性最优化问题（Verhoeye and Wulf，2002；张洪恩等，2006）。假设线性混合分解得到C类地物的百分比图像，每个低分辨率的像元被分解成N 个子像元，与地物百分比相对应的第i类地物的子像元数为NCi，Cij表示i 类地物在子像元j 位置上的空间依存度，子像元被赋予1或0，表示属于或不属于某类地物，那么，现在问题就是怎样确定子像元的值使得像元的空间依存度最大。为此，构造数学模型，定义变量Xij，其中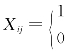
，则在限制条件下：
数学模型可以表示为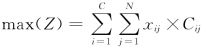
，计算每一类在每一个子像元上的空间依存度。设低分辨率的百分比图像有M 个像元，用像元中心的位置作为它们的位置，则子像元的空间依存度可以表示为：
式中：wk 为子像元到像元中心距离的函数；(www.xing528.com)
fk 为像元百分比。
在实际应用中，并不需要考虑图像中所有像元，由于距离越远，空间联系越小，因此只需考虑一定距离范围内的像元即可。由于目标函数和限制条件都是线性方程，所以把寻找方程的解变成线性最优化问题。当前，寻找线性最优解有各种各样的方法，以下引入一种新的理论模型，解决线性最优解的问题。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
