基于非监督神经网络的亚像元定位方法优化

与监督型神经网络不同，利用非监督型Hopfield神经网络模型也可以完成遥感影像的亚像元定位。该神经网络模型主要是引入了“能量函数”的概念，通过自身的不断调节，寻求能量最小的最优解，并给出了网络稳定性判据（Tatem 等，2001）。采用非监督性能量聚集神经网络模型Hopfield神经网络来模拟亚像元的位置分布，具体分为如下几个方面。

1.Hopfield神经网络的初始化

给网络中各神经元赋初值时，应遵循以下两条原则：

（1）确定对应低分辨率图像中同一像素的一组神经元，并随机地给该组中一定比例的神经元赋初始值，该比例和原来像素中的类别比例相等，给神经元组中剩余的神经元赋予uinist=0.45的初始值。选择0.55和0.45作为初始值，实际上是给各神经元设定了一种初始的开、关状态。这样的取值主要是处于节省时间的考虑。

（2）完全随机地给神经元赋予［0.45，0.55］之间的一个初始值。这样便可以与按类别比例进行的初始化进行对比，并且由于没有利用类别估计的结果，这种初始化过程并不会引入额外的误差。

2.定义能量函数

能量函数是通过目标函数和约束条件的组合定义的，即：

式中：k1、k2、k3 为加权求和的权值；

G1ij、G2ij为两目标函数的输出；

Pij为比例约束神经元的输出。(www.xing528.com)

3.定义目标函数

几乎所有自然或人造的场景都具有一定程度的空间连续性。具体来说，在图像中邻近像素间的相似性一般大于较远的像素间的相似性，其不相似的程度与环境及所观察物体的特性有关。在这种情况下，需要使一个神经元的输出能与邻近神经元的输出相似。当神经元neuron（i，j）的输出和8个邻近神经元输出的平均值相似时，给出较低的能量，否则就认为网络产生较高的能量。但是，要生成二值图像，仅满足邻近神经元输出相似是不够的，因此，引入了两个目标函数：一个旨在增大神经元的输出（使输出趋近于1）；另一个旨在减小神经元的输出（使输出趋近于0）。如果邻近8个像素的平均输出大于0.5，第一个目标函数就将中心神经元的输出增大，使之逼近1。

式中λ控制了函数的陡峭程度，而tanh函数则控制了邻近神经元的作用。如果邻近神经元的平均输出小于0.5，式（5-4）的取值将向0逼近，这样该函数对式（5-3）表示的能量函数几乎没有任何影响。如果平均输出大于0.5，式（5-4）的取值就会向1逼近，（vij-1）函数控制了负梯度输出的幅度，零梯度只有在vij=1时可以取得。梯度为负值，神经元的输出将增大。当周围8个神经元的平均输出小于0.5时，第二个目标函数将中心神经元的输出由1递减到0。

这里，当周围神经元的平均输出大于0.5时，tanh函数的取值将逼近0，而当tanh 函数的取值小于0.5 时，函数取值将逼近1，中心神经元的输出决定了整梯度输出的幅度，只有当vij=0时才取零梯度。 当梯度为正时能量函数将减小。 只有当vij = 1 且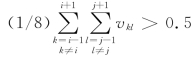，或vij=0 且 时能量函数才等于零，此时G1ij+G2ij=0。这和要产生空间连续性的目的是一致的，同时神经元的输出将逐渐逼近0或1，从而生成一幅二值图像。

4.考虑比例约束

目标函数增强了空间连续性，但是仅使用目标函数会使所有的神经元的输出只取0或者1，因此，需要将目标函数的作用限制在一定区域内。比例约束Pij正是基于这样的考虑而引进的，设计它的目的是为了保持模糊分类得到的像素内的类别比例。这一目标可以通过限定一组神经元的总输出和它们所对应的原始像素点的预测比例值相等来实现。下面，引入一种区域比例估计函数，它表示一组神经元中所有取值大于或者等于0.55的神经元所占的比例。

tanh函数可以保证在神经元的输出大于0.55的情况下，其输出可以看作1，并认为它位于一类的估计区域内。当输出小于0.55时，该神经元不包括在估计范围内，这样便可以简化估计过程，并且限定了神经元的输出必须超过初始分配的0.55，才能进入计算的范围。为保持模糊分类得到的各像素内的类别比例，将每一像素的类目标比例axy从区域比例估计式（5-6）中减去：

当像素（x，y）的区域比例估计小于目标区域时，式（5-7）会产生一个负梯度，这样便会增大神经元的输出进行弥补。分类估计的过估计会产生正梯度，相应地会导致神经元输出的减小，只有当区域比例估计和目标区域估计完全一致时，才会产生零梯度。