影响基于神经网络的亚像元定位算法的两个重要参数分析

为了对上述基于神经网络的亚像元定位算法进行更加有效的分析，本书分别选择了影像类别个数和重采样尺度大小两个参数，通过分析两个参数的变化，来判断它们对结果误差的影响。这里把误差定义为：以原始高分辨率影像的分类结果作为真实数据，与BP、ARTMAP神经网络模型的定位结果相比较后，被错误分类的亚像元所占的百分比值。

1.类别个数影响

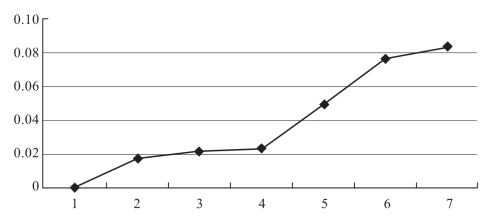
在地物类别个数增加的情况下，混合像元中的每个亚像元将会更多地受到不同“吸引力”的影响，这些“吸引力”来自于不同的地物类别。如何保持各种“吸引力”的平衡，确定亚像元的值，将会变得复杂，这使得利用该模型进行亚像元定位的误差增大。图5-6和图5-7表示在类别个数增加时，对应误差值的变化情况。可以看到，当类别个数较少时，误差变化比较小，当类别个数增加到6时，误差相应地增加到最大。

2.尺度选择影响

尺度的选择与本书的研究结果有着密切的关系，由于本书的实验是采用合成图像来模拟混合像元分解后的丰度图，并以此作为亚像元定位模型的输入数据。所以，选择不同的尺度来对原始影像的硬分类结果进行均值滤波处理（重采样），可以获得不同的低分辨率丰度影像，用以检测两种神经网络模型的有效性。如图5-8所示，当尺度选择为3，5，7，9的时候，中心像元对应于不同尺度上的亚像元及其8邻域分布情况，其中的1个像元分别包含了原始影像中3×3，5×5，7×7，9×9个亚像元。

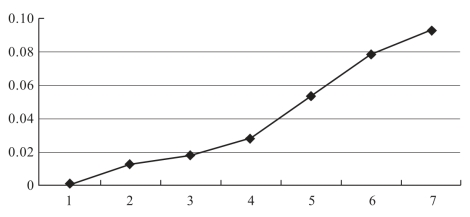
图5-6　BP神经网络对应不同类别数的误差分布图

(www.xing528.com)

图5-7　ARTMAP神经网络对应不同类别数的误差分布图

图5-8　尺度S=3，5，7，9时所对应的不同个数的亚像元

当尺度选择的越大时，混合像元中增加的亚像元个数越多，定位信息量增加，满足空间相关性最大的条件变得更加复杂，最终亚像元定位结果的误差越大，这在图5-9中得到了证实。

综上所述，利用Fuzzy ARTMAP神经网络模型求解亚像元定位要比利用BP神经网络模型效果精度要高。原因在于：BP神经网络模型算法本质上为梯度下降法，所要优化的目标函数又非常复杂，因此结果中必然会出现“锯齿形现象”，这会使得BP算法低效；另外由于网络的训练过程耗费时间较长，容易陷入极大或极小，收敛不完全对结果也会造成一定的影响。与其相比较，Fuzzy ARTMAP神经网络模型具有结构简单、计算量小、适应性强等特点。

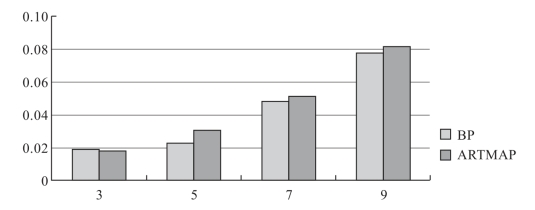
图5-9　不同尺度因子下的误差对比图

另外，利用这两种神经网络模型来估计亚像元的位置，在类别个数增加和模糊尺度增大的情况下，像元空间关系更加复杂，误差会相应地增大，如何更精确地获取亚像元的空间分布，仍需要进一步开展研究工作。