线性模型是最简洁、应用最广泛的光谱混合模型，以线性混合模型为基础的光谱混合分析技术（SMA）已经应用到各个领域。线性模型一方面利用多光谱影像波段大于端元数的特点进行像元分解，另一方面也可以利用多时相遥感影像进行像元分解。模型计算的结果为各端元的分量图像和一幅表征均方根误差的残差图像（吴波，2006）。
在线性模型中，将像元在某一波段的光谱反射率表示为占一定比例的各个终端单元（Endmember）反射率的线性组合，设r是大小为m×1的像元光谱矢量，S=［s1，s2，…，sk］是大小为m×K 的端元光谱矩阵，α=［α1，α2，…，αK］T 是k 维矢量，其各分量元素为对应像元组分，e为m 维随机噪声，且满足e～N（0，1）的独立分布。
则线性混合像元模型为：
因此，第i波段像元反射率γi 可以表示为：
式中：i=1，2，…，m，j=1，2，…，n；
γi 为混合像元第i个波段的反射率；
aij为第i个波段第j 个端元组分的反射率；
xj 为该像元第j 个端元组分的丰度；
ei 是第i波段的误差；
m 为波段数；
n为选定的端元组分数。
假设端元光谱矩阵S 已知，则混合像元的最小二乘估计是在噪声能量e为最小条件下，得出组分α 的最优估计。(www.xing528.com)
式中：‖·‖表示对矢量求范数，它定义为对应矢量的点积。因此式（3-3）可以写为：
定义能量：
对J 求偏导，求出组分α 的估计值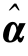
：
因此，
由于S 为端元光谱矩阵，其各列元素为不同纯净地物的光谱响应值，它们是相互线性独立的，因此如果S 的列数小于行数，即端元数目小于波段数目时，自相关矩阵的逆（STS）-1总是存在的，因而能够估计出各地物组分值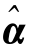
。
从上面的推导可以看出，在估计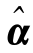
的值时，假设e～N（0，1）的独立分布的条件是不必要的。但为了简化下面的推导，在推导过程中还是附加了这个限定。
这时，像元光谱矢量r的估计值为：
因此像元的光谱误差为：
为评价该分解模型，通常用光谱残差E 均方根误差定量表示：
可以通过几种方法求得单个像元内各个端元组分丰度xj。同时还应当受到下面的条件限制：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
