优化Hopfield神经网络模型的标题

Hopfield（1982）利用非线性动力学系统理论中的能量函数方法研究反馈人工神经网络的稳定性，并利用此方法建立求解优化计算问题的系统方程式，提出了可用作联想存储器的互连网络，这个网络称为Hopfield 网络模型，也称Hopfield模型，并成功地被应用于TSP 等经典NP 难题的研究中，极大地推动了神经网络的发展（王建华，1999；周成虎等，1999）。Hopfield网络模拟人的神经系统结构和人脑的信息处理功能，在优化计算、信息压缩和模式识别领域取得了广泛的应用。

Hopfield神经网络模型是一个由非线性元件构成的全连接型单层反馈系统，从输出到输入都有反馈连接（图2-8）。所以，Hopfield网络在输入的激励下，会产生不断的状态变化。当有输入之后，可以求取Hopfield的输出，这个输出可以反馈到输入从而产生新的输出，这个反馈过程一直进行。如果Hopfield网络是一个能收敛的稳定网络，则这个反馈与迭代的计算过程所产生的变化越来越小，一旦到达了稳定平衡状态，Hopfield网络就会输出一个稳定的恒值。通常，Hopfield网络分为离散型和连续型两类。

1.离散型Hopfield网络

离散型Hopfield神经网络由N 个神经元互连而成。神经元的输出为离散值1或0，它们分别代表神经元的激活和抑制状态。这种神经网络的各神经元相互连接，其连接强度用权值表示，N×N 维矩阵称之为权矩阵。每个神经元都有一阈值（或称门限值）。权矩阵和阈矢量就定义唯一一个N 维的离散型Hopfield神经网络。对于一个离散的Hopfield网络，其网络状态是输出神经元信息的集合。对于一个输出层是n 个神经元的网络，其t时刻的状态为一个n 维向量：

所以网络状态有2n个状态。因为Yj（t）（其中j=1，2，…，n）可以取值为1或0，故n维向量Y（t）有2n种状态，即网络状态。

图2-8　Hopfield神经网络的结构图

离散型Hopfield网络是一种多输入含有阈值的二值非线性动力系统。在动力系统中，平衡稳定状态可以理解为系统某种形式的能量函数在系统运动过程中其能量值不断减小，最后处于最小值。(www.xing528.com)

2.连续型Hopfield网络

连续型Hopfield神经网络同样由N 个神经元互连而成，但神经元的输出不再是离散值0或1，而是可以在某一区间连续变化。这种拓扑结构与生物神经系统中大量存在的神经反馈回路相一致，与离散型Hopfield网络的结构相同。两种类型网络的共同点是：连续Hopfield网络的稳定条件也要求Wij=Wji。不同之处在于：其函数g 不是阶跃函数，而是S型的连续函数。一般取：

连续型Hopfield网络在时间上是连续的。所以，网络中各神经元是处于同步方式工作的。Hopfield工作时其各个神经元的连接权值是固定的，更新的只是神经元的输出状态。

3.Hopfield网络优化规则

Hopfield神经网络的运行步骤为：首先从网络中随机选取一个神经元ui，进行加权求和；然后再计算ui 的第t+1时刻的输出值。若除ui 以外的所有神经元的输出值保持不变，则返回至第1步，直至网络进入稳定状态。网络中的每一个神经元都将自己的输出通过连接权传送给其他所有神经元，同时又都接收其他所有神经元传递过来的信息。即：网络中的神经元t时刻的输出状态实际上间接地与自己t-1时刻的输出状态有关。所以，Hopfield神经网络是一个反馈型的网络，其状态变化可以用差分方程来表征。利用神经网络进行优化计算，就是在神经网络这一动力系统中给出初始的估计点，即初始条件；然后随网络的运动传递而找到相应极小点。反馈型网络的一个重要特点就是它具有稳定状态。当网络达到稳定状态，它的能量函数达到最小。这里的能量函数不是物理意义上的能量函数，而是在表达形式上与物理意义上的能量概念一致，表征网络状态的变化趋势，并可以依据Hopfield工作运行规则不断进行状态变化，最终能够达到的某个极小值的目标函数。如果把一个最优化问题的目标函数转换成网络的能量函数，把问题的变量对应于网络的状态，那么Hopfield神经网络就能够用于解决优化组合问题，这样大量的优化问题都可以用连续的Hopfield网络来求解。表2-1中简单地列举了3种常用的神经网络类型的对比。

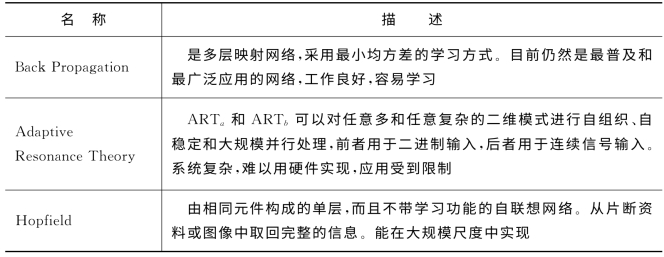
表2-1　3种常用的神经网络模型的描述