早在20世纪40年代初期,心理学家McCulloch、数学家Pitts就提出了人工神经网络的第一个数学模型,从此开创了神经科学理论的研究时代(McCulloch,1943)。美国神经科学家Hecht Nielsen(1989)给出了一个人工神经网络的一般定义:神经网络是由多个非常简单的处理单元彼此按某种方式相互连接而形成的计算机系统,该系统是靠其状态对外部输入信息的动态响应来处理信息的。神经网络是由神经元组成,一个神经元的信息处理一般包括3个部分:输入信号、连接权重和激活函数(也称作用函数)。简化的神经元的基本工作机制是一个神经元有两种状态:兴奋和抑制。平时处于抑制状态的神经元,其树突或胞体接受其他神经元经由突触传来的兴奋电位,多个输入在神经元以代数和的方式叠加;如果兴奋总量超过某个阈值,神经元就会被激发进入兴奋状态,发出脉冲信号,并由轴突的突触传递给其他神经元。简单的神经元网络是对生物神经元的简化和模拟,其模型见图2-2。

图2-2 模仿大脑神经网络模型
人工神经元是神经网络的基本处理单元(李孝安,1995)。它是一多输入、单输出的非线性元件,其输入输出关系可以描述为:

式中:xj(j=1,2,…,n)是从其他细胞传来的输入信号;
θi 为阈值(Threshold),又称为门限,一般它连接至固定偏置1;
wji是从细胞j 到细胞i的连接权值;
Si 为神经元i的净输入;
f(·)为转移函数(Transfer Function)。
神经元又称为节点,它只模仿了生物神经元所具有的大约150多个功能中的最基本、最重要的3个:①加权,即可对每个输入信号进行程度不等的加权;②求和,即确定全部输入信号的组合效果;③转移,即通过转移函数f(·)确定其输出。尽管只模仿了这3个功能,人工神经元构成的网络仍然显示了很强的生物原型特性,这是因为抓住了生物神经元的基本特性。转移函数f(·)又称激活函数(Activation Function),其作用是模拟生物神经元所具有的非线性转移特性,是单调上升函数,而且必须是有界函数。
因为细胞传递的信号不可能无限增加,必有一最大值,所以常用的激活函数最主要有3种(孙德保和高保,1994;蔡国平等,1998)。
(1)阈值函数。这种激活函数见图2-3,可以写成:
 (https://www.xing528.com)
(https://www.xing528.com)
常称这种神经元为M-P模型。
(2)分段线性函数。分段线性函数见图2-4,即:

其中,在运算的线性区域内放大因子置为1。这种形式的激活函数是对非线性放大器的近似。
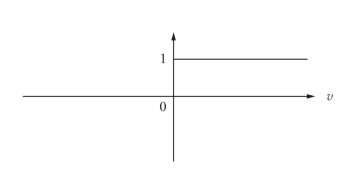
图2-3 激活函数1

图2-4 激活函数2
(3)Sigmoid函数。此函数的图形是S形函数,在构造人工神经网络中是最常用的激活函数。它是严格的递增函数,在线性与非线性之间显现出较好的平衡。它的一个典型例子是Logistic函数,定义如下:
![]()
其中,a为Sigmoid函数的倾斜参数。改变参数a 就可以改变倾斜程度(图2-5)。在极限情况下,倾斜参数趋于无穷,Sigmoid函数就变成简单的阈值函数。阈值函数仅取-1 或1,而Sigmoid函数的值域是-1到1的连续区间。还要注意到Sigmoid函数是可微分的,而阈值函数不是。可微性是神经网络理论的一个重要特征。这种情况下激活函数是关于原点反对称的,也就是说,激活函数是v的奇函数。
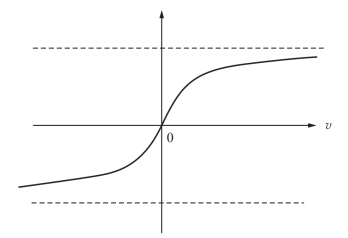
图2-5 激活函数3
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




