流体在亚临界和超临界状态的热物性存在明显差异,图7-11(a)所示为压力为9 MPa时超临界CO2的密度、定压比热容、热导率和黏度随温度的变化曲线。可以看出,在临界温度附近,这些热物性出现很大的波动。图7-11(b)所示为不同压力下CO2的定压比热容随温度的变化曲线,在临界点附近,定压比热容急剧增大。热物性的明显变化会影响传热计算的精度,在实际工作中,需要根据CO2所处的状态,选用合适的传热关联式来进行传热计算。
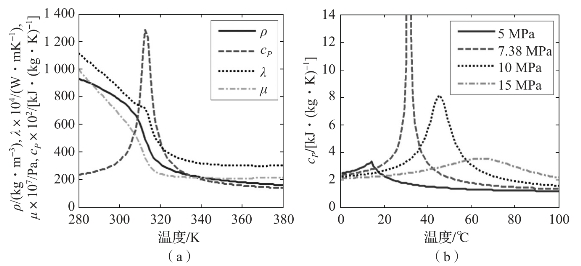
图7-11 CO2热物性随温度的变化曲线
(a)压力为9 MPa时的热物性;(b)不同压力下的定压比热容
在二氧化碳动力循环的热力学分析中,常常需要估算换热器面积的大小,这对计算系统的尺寸和成本很关键。因此,需要计算CO2在不同形式换热器中的对流传热系数。对于管壳式换热器,对超临界状态的二氧化碳可采用Krasnoshchekov-Protopopov关联式[9]计算。
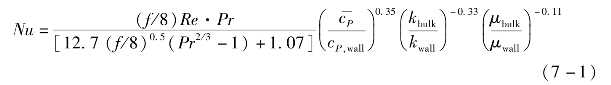
式中,Re和Pr为工质的雷诺数和普朗特数;摩擦因子f=(1.82 lg Re-1.64)-2;k为导热系数;μ为黏度;下标“bulk”指流体平均温度,下标“wall”指壁面温度;![]() 为按截面平均的定压比热容,
为按截面平均的定压比热容,![]()
亚临界状态单相CO2的换热可采用Petukhov关联式[10]计算。
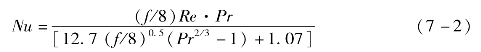
在求得摩擦因子f后,可由式(7-3)求得换热器的压降:

式中,G为质量流量,L为流道长度,D eq为水力直径。
气液两相状态的对流换热系数可由Cavallini-Zecchin关联式[11]求得。
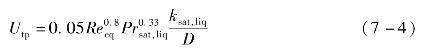
式中,Re eq由下式给出:
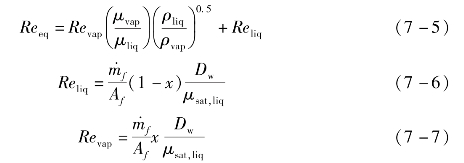
冷凝器内CO2工质的压降可由Kedzierski-Goncalves关联式[12]计算。
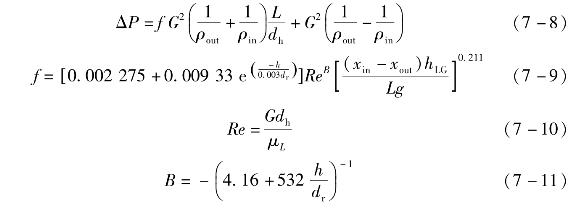
近年来,对超临界CO2与高温热源换热的换热器可采用印制电路板式换热器(Printed Circuit Heat Exchanger,PCHE),PCHE内CO2的对流传热系数可由Gnielinski关联式[13],[14]求得。
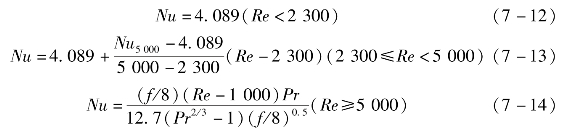
PCHE内部微通道内的压降与Re和管内壁粗糙度有关,设壁面的蚀刻轮廓波峰与波谷间的最大轮廓高度为δ,则相对粗糙度定义为
![]() (https://www.xing528.com)
(https://www.xing528.com)
根据相对粗糙度确定的流动过渡区雷诺数为
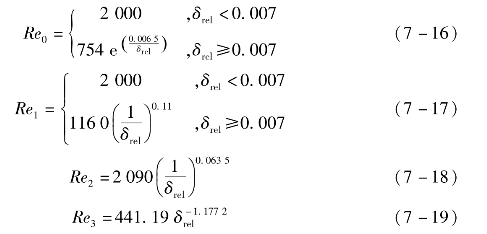
当实际流动雷诺数Re小于Re0时,

当Re0<Re<Re1时,
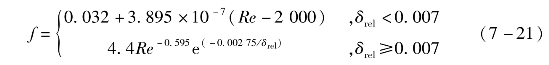
当Re1<Re<Re2时,
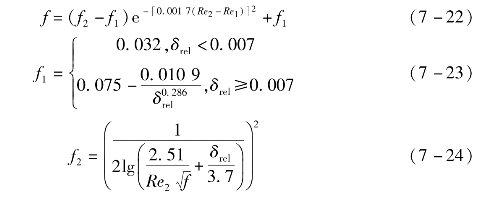
将式(7-23)和式(7-24)代入式(7-22),通过迭代求解可得f,f的初值由下式给出:

当Re2<Re<Re3时,
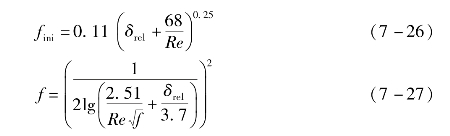
当Re>Re3时,
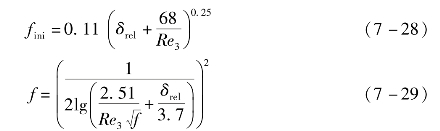
对采用CO2的工质泵,不同工况下的性能可由相似定律进行估算。

工质泵的工作效率可由下式估算:
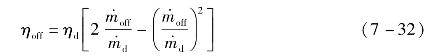
对于截面不可调整的涡轮膨胀机,当采用压力滑移模式工作时,在不同工况下可由Stodola椭圆公式[15]近似计算其工作性能。
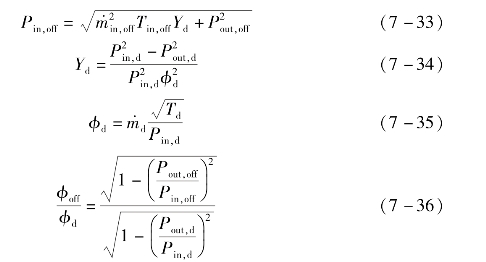
涡轮效率可由下式估算[16]:
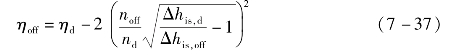
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




