氨水非共沸混合工质的热物性及传热计算

氨作为一种不含碳原子的天然工质，其比热容较低，临界压力比有机工质高，GWP值小于1，是一种环境友好型工质。但是，氨具有易燃性、毒性和腐蚀性。氨蒸气在空气中易燃，空气中混有18%～28%的氨蒸气即可燃烧，甚至发生爆炸，加热到热解温度可释放出有毒的烟气。氨还会损伤人的皮肤、眼睛和鼻子［1］。氨对纯铜、黄铜、锌合金和钛合金具有腐蚀作用，对铝、氧化铝陶瓷、铸铁、不锈钢等的腐蚀性很小。氨的生产和运输技术已经很成熟，当前全球每年生产和运输的氨达到1.8亿t。

氨水混合物的热物性可根据吉布斯自由能进行计算［2～5］。纯工质的吉布斯自由能为

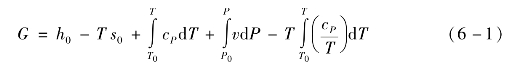
单组分液体的定压比热容可表示为

对应比容可表示为

代入式（6-1），可得到液态的相对吉布斯自由能为

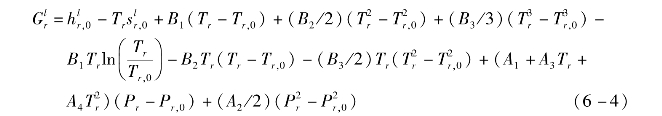
气态的相对吉布斯自由能为

式中，下标“0”表示理想气体状态。Tr、Pr和Gr为实际值相对参考点之间的比值。

下标B表示参考点。

纯组分的摩尔比焓、比熵和比容可由吉布斯自由能求得。

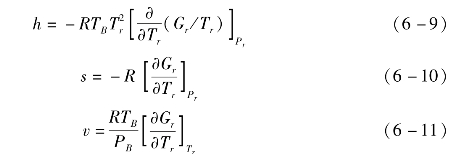
氨水混合物的热物性可根据相同热力状态的氨和水的热物性求得。气态氨水混合物的比焓、比熵和比容为

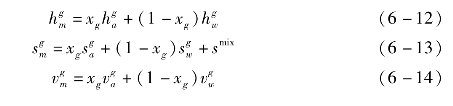
对于液相有

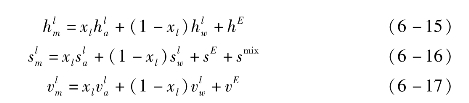
式中的剩余属性可由剩余吉布斯自由能求得：

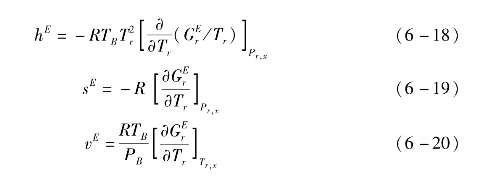
气体混合熵为

氨水混合物的相对剩余吉布斯自由能为

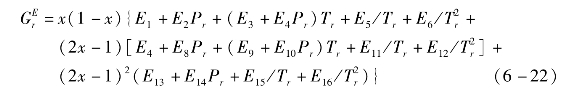
对于气液两相状态的氨水混合物，定义其干度为

则气液两相状态氨水混合物的热物性可表示为

对于氨水非共沸混合物，采用Refprop计算热物性时，在接近露点和泡点的区域迭代计算可能会出现发散现象。因此，在压力和氨质量分数x已知的情况下，可由Patek-Klomfar经验公式［6］求得相应的泡点和露点温度，其中泡点温度的计算公式为

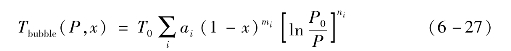
露点温度的计算公式为

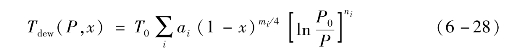
利用上面的方法可求得氨水混合物在不同压力下的露点温度和泡点温度，如图6-1所示。压力一定时，随着氨质量分数的增加，对应的泡点温度和露点温度均逐渐减小。同时，氨质量分数一定时，露点温度总是高于对应的泡点温度，二者的差值为温度滑移。随着氨质量分数的增加，温度滑移先逐渐增加后逐渐减小，存在一个氨质量分数使对应的温度滑移最大。随着压力的增大，对应的露点线和泡点线逐渐向温度高的方向移动。

图6-1　氨水混合物的泡点温度和露点温度

氨水混合物在换热器内部的流动和对流换热过程中，通常采用经验传热关联式计算对流传热系数，氨水混合物的输运属性和对流传热系数的计算精度对换热器尺寸和设计影响很大。当前计算氨水混合物的输运属性主要有两种方法：（1）插值方法，根据同等温度和压力下的纯组分的属性值通过插值方法计算氨水混合物的输运属性；（2）对比态方法，根据氨水混合物的拟临界参数计算其输运属性。插值方法精度较高，但在某些气液两相区域无法进行计算，对比态方法可计算各种状态，但相对精度较低。计算液态和气态氨水混合物输运属性的主要方法见表6-1和表6-2。

表6-1　液态氨水混合物输运属性的计算

续表

表6-2　气态氨水混合物输运属性的计算

续表

续表

基于Mishara关联式的Rivera-Best方法和Khir方法可计算管内氨水混合物流动的沸腾传热。设k、ρ、μ、x为流体的热导率、密度、动力黏度、干度；G为质量通量；q为热通量；d为管径；h LV为蒸发潜热，下标L和V分别表示饱和液态和饱和气态。h L为液态对流传热系数，则Mishara关联式可表示为

式中

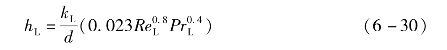
X tt为Lockhart-Martinelli数：

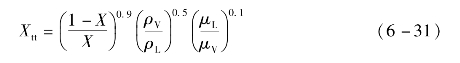(www.xing528.com)

Bo为沸腾数：

Re L为液态雷诺数：

由于试验条件的压力、热流密度、氨质量分数、氨水混合物干度等参数存在很大不同，不同关联式得到的拟合常数可能存在较大差异。在Rivera-Best方法中，［c，m，n］=［65，0.5，0.15］，Khir方法则采用［c，m，n］=［5.64，0.23，0.05］。

对核态池沸腾关联式进行扩展也可得到流动沸腾传热关联式。Arima等得到的氨水核态池沸腾传热关联式为

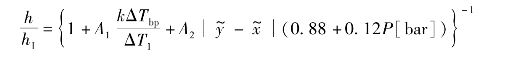
式中，h I为理想传热系数，可由各纯组分的核态传热系数得到：

Taboas等拟合的关联式为

Inoue-Monde关联式为

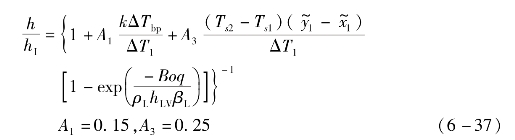
在得到核态池沸腾对流传热系数后，可采用Gungor-Winterton方法计算流动沸腾传热系数。

式中，E2根据Froude数Frf0确定。

采用经典的宽沸腾关联式也可计算氨水的流动沸腾传热系数。Wettermann-Steiner关联式为

Jung等提出的关联式为

图6-2所示为针对上述几种方法计算的流动沸腾传热系数［18］，计算时氨质量分数为0.5，压力为4 bar，管内径为34 mm。采用Rivera-Best方法计算的流动沸腾传热系数明显大于其他方法，采用Khir等的拟合关联式计算的结果明显小于其他方法。剩下5种方法估算的流动沸腾传热系数之间的差别较小。流动沸腾传热系数随着热通量和质量通量的增加而增大。在大部分条件下核态沸腾的贡献较小，只有在低干度、小质量通量或高热通量条件下贡献较大。Karn等通过对比分析推荐对液态的动力黏度和热导率采用Conde-Petit方法，对气态动力黏度和热导率计算采用Wilke和Mason-Saxena方法，针对动态仿真，建议采用基于对比态的Chung等的方法［19］。

图6-2　不同流量和热流密度下流动沸腾传热系数随干度的变化曲线［18］

关于氨水混合物在管内流动传热的研究已有很多，但在板式换热器内的传热研究相对较少。Taboas等研究了垂直板式换热器内氨水的对流换热特性［20］，试验的氨水的热通量为20～50 kW/m2，质量通量范围为70～140 kg/（m2 s），平均干度范围为0～0.22，压力范围为7～15 bar，氨质量分数范围为0.42～0.62。在试验的范围内，流动沸腾传热系数与质量通量相关性大，随着质量通量的增大而明显增加，但是在干度较大时，热通量和压力对流动沸腾传热系数的影响很小。板式换热器的压降随质量通量或干度的增加而增大，与热通量基本不相关。Arima等也研究了浓氨水在垂直板式换热器内的传热特性［21］，试验的氨质量分数为0.9，质量通量范围为7.5～15 kg/（m2 s），热通量范围为15～23 kW/m2，压力范围为7～9 bar。结果显示流动沸腾传热系数随着质量通量或干度的增加而增加，随热通量的增加而减小。

Taboas等分析了不同传热关联式对氨水混合物对流传热的预测精度［22］，发现Donowski-Kandlikar和Han等采用的关联式预测精度较高。Donowski-Kandlikar的流动沸腾传热关联式［23］为

式中，对流数Co为

E CB和E NB分别为对流沸腾和核态沸腾增效因子，根据数据拟合结果为E CB=0.512，E NB=0.338。

Han等根据采用R410a和R22的板式换热器试验数据，提出包含换热器几何参数的努塞尔数Nu关联式［24］如下：

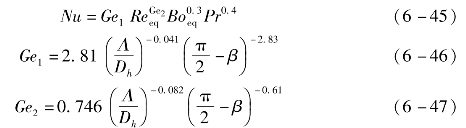
式中，Ge1和Ge2为无尺度几何参数，Λ为波纹节距，Dh为水力直径，Re eq和Bo eq为等效雷诺数和等效沸腾数。

板式换热器的压力损失计算方法有Chisholm方法、基于单位体积动能的KE方法和等效雷诺数方法。Chisholm方法基于Lockharte-Martinelli数X和两相摩擦因子φ1计算［25］。

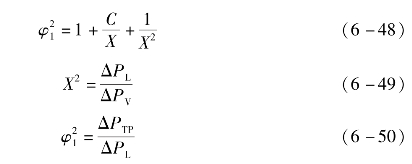
式中，ΔP L和ΔP V为液态和气态压降，C为拟合常数。

Longo和Gasparella基于R134a、R410a、R236fa等的垂直板式换热器试验数据拟合的KE关联式［26］为

等效雷诺数方法根据两相摩擦因子来计算压降：

式中，G为质量通量，L为流道长度，vm为流体平均比容。

Han等采用包含换热器几何参数的经验公式［24］来计算两相摩擦因子：

Taboas等的计算结果显示，3种方法中Chisholm方法预测的压降与试验数据吻合度最高。随后，Taboas等根据流动形态的不同提出了一个两阶段关联式，分别对应核态沸腾占优和对流沸腾与核态沸腾并存两种流动模式。首先流动过程中，液态的表观流速为

气态的表观流速为

如果u SV＜-111.88u SL+11.848，此时核态沸腾传热占主导：

如果u SV≥-111.88u SL+11.848，此时核态沸腾和对流沸腾并存：

Mergner和Schaber研究了板式蒸发器内氨水的蒸发过程［27］，通过分析设备运行5年的记录数据，发现板式蒸发器内的压降、干度和传热能力主要受到蒸发器内的工作压力、温度和质量流量的影响，而氨的质量分数变化影响很小。Koyama等研究了氨工质在采用微翅表面的钛金属板表面的传热性能［28］。选取的试验条件：质量通量为5和7.5［kg/（m2 s）］，热通量为10、15和20（kW/m2），流道高度为1、2和5（mm），饱和压力为7和9（bar）。研究发现采用微翅结构可以提高板式换热器的换热能力，横向翅的扰流作用强，湿区面积大，有利于核态沸腾，因此横向翅的强化传热能力优于纵向翅。在试验的雷诺数小于443范围内为层流，微翅板式换热器的对流传热系数随着质量通量、热通量和饱和压力的增加而增大，随着流道高度的增加而减小。