工质与热源的匹配原则与应用技巧

整个ORC系统的工作效率受到有机朗肯循环热效率的限制，还受到蒸发器内工质与热源之间换热过程的热回收效率影响。因此，针对具体的热源，有必要对工质与热源之间的温度匹配情况进行分析。根据具体应用场合的不同，ORC系统在进行工质选择时需要考虑工质临界温度等热物性与热源的匹配。通过分析蒸发器内工质与热源之间的换热过程，可以更详细地了解整个吸热过程的热回收效率，以及ORC系统工作参数变动对吸热过程和ORC系统工作性能的影响。

夹点分析法是分析工质与热源匹配情况的有力工具，根据设定的夹点温差，对工质与热源之间的换热过程进行分段计算，可以确定具体的夹点位置，以及整个换热过程的温度匹配情况。以亚临界ORC系统为例，可分析热源温度与工质临界温度之间的匹配特性。图2-1所示为采用R1234yf工质的亚临界ORC系统的热效率和比净输出功率随蒸发温度的变化曲线［1］。随着蒸发温度的增加，ORC系统的热效率单调上升，但是比净输出功率在靠近临界温度时出现逐渐下降趋势，存在一个最优的蒸发温度使比净输出功率最大。这是因为随着蒸发温度升高，对应的蒸发压力增大，有机朗肯循环热效率增大，但进一步增大蒸发压力，会导致蒸发器的热回收效率下降。因此，对于亚临界ORC系统来说，当蒸发温度位于临界温度附近某个最优值时，比净输出功率最大。

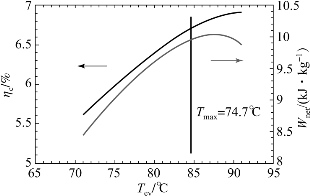
图2-1　ORC系统性能随蒸发温度的变化［1］

对采用纯工质的亚临界ORC系统，工质临界温度与热源入口温度的差值会影响蒸发器内的夹点温差位置。当热源入口温度远高于工质临界温度时，蒸发器内的夹点出现在工质入口处。随着热源入口温度与工质临界温度的差值逐渐减小，夹点会转移到饱和液态状态点。两种情况的夹点位置如图2-2所示。只有当热源入口温度与工质临界温度的差值处于某一个优化值附近时，蒸发器内的热回收效率才会达到最大值。

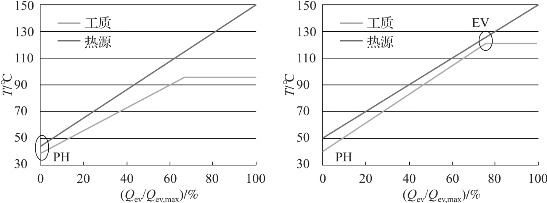
图2-2　亚临界ORC系统工质与热源之间的换热［1］

（a）夹点位于工质入口处；（b）夹点位于工质饱和液态状态点

定义热源入口温度与工质临界温度的差值为

设使ORC系统比净输出功率最大的蒸发温度（最优系统蒸发温度）为T ev，S，opt，定义最优循环蒸发温度与最优系统蒸发温度的差值为

针对温度为150℃的地热水，不同工质的优化计算结果如图2-3所示。图2-3（a）所示为最优系统蒸发温度、最优循环蒸发温度以及两种蒸发温度差值随工质临界温度的变化，图2-3（b）所示为循环热效率ηc、热回收效率εhr和系统总热效率ηsys的结果。随着工质临界温度与热源入口温度差的变化，两种最优蒸发温度的差和系统总热效率均呈现有规律的变化。

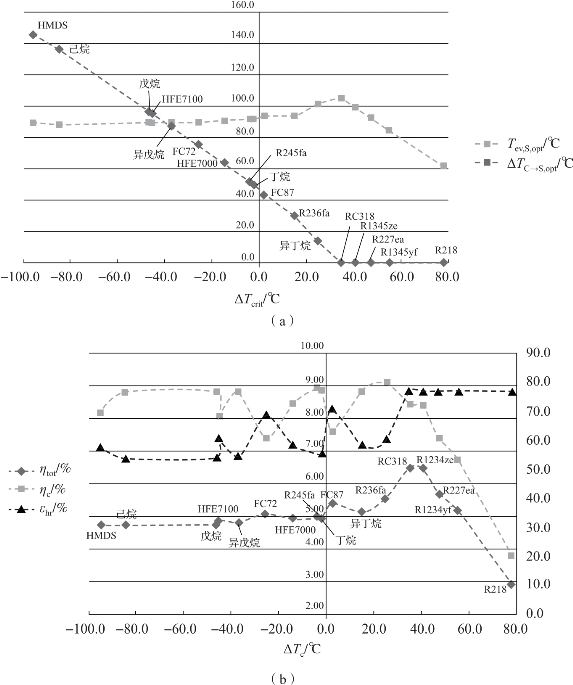
图2-3　亚临界ORC系统性能随工质临界温度的变化［1］

（a）T ev，S，opt与ΔT C→S，opt；（b）　循环热效率、热回收效率和系统总热效率

（1）当工质的临界温度很低时，ΔT crit＞40℃～45℃，蒸发器内换热温差夹点位于工质入口处，ΔT C→S，opt=0，最优循环蒸发温度等于最优系统蒸发温度。此时，随着工质临界温度的升高，系统循环热效率会逐渐增加而热回收效率不受影响，但由于此时工质的临界温度偏低，系统总热效率仍然较低。

（2）当工质临界温度接近热源入口温度时，蒸发器内的温差夹点位置会从工质入口处转换到饱和液态状态点处。随着工质临界温度的升高，最优循环蒸发温度逐渐增大，而最优系统蒸发温度受到热源温度的限制基本保持不变，ΔT C→S，opt会逐渐增大。系统总热效率最大需要对循环热效率和热回收效率进行平衡，当夹点正好从热源入口转换到饱和液态状态点时，系统总热效率最大。此时的工质临界温度约比热源入口温度低35℃。

（3）当工质临界温度进一步增大时，ΔT C→S，opt继续呈线性增大，意味着无法同时满足最优循环热效率和高的热回收效率的要求，此时最优系统蒸发温度基本保持在恒定值，约为90℃。而对于不同工质而言，当蒸发潜热较大时，循环热效率较高，而此时的热回收效率会较小，反之亦然。总体上，系统总热效率有轻微减小的趋势。

采用夹点分析法不仅可以判断工质与热源之间的温度匹配情况，还可以对蒸发器的换热面积进行估算，进而评估ORC系统的经济性。对夹点分析法的每一段换热过程，采用对数平均温差法，结合具体的传热关联式，可以对每一段的换热面积进行计算。由于蒸发器内存在相变过程，其换热过程包括热源与单相工质的换热以及热源与气液两相工质的换热。在具体应用时需要选择合适的传热关联式，注意具体的应用条件范围，最好利用试验对传热关联式的精度进行验证。尤其对工质的气液两相换热过程，传热关联式的精度可能存在较大误差。例如，针对生物质发电应用，Weith等分析了采用MM和MDM的非共沸混合工质的对流换热系数计算精度［2］；对蒸发器内的换热过程，采用Kandlikar关联式［3］，［4］估算了预热器和蒸发器面积。预测硅氧烷类高温工质在不同蒸气干度和质量流量下换热系数的变化趋势时，直管内的流动沸腾换热系数可表示为

式中，核态沸腾换热系数为

(www.xing528.com)

对流沸腾换热系数为

式中，x为蒸气干度，Co为对流数，Bo为沸腾数，F Fl为流体表面参数。

对于单相换热系数，当0.5≤Pr L≤2 000且104≤Re LO≤5×106时，采用Petukhov-Popov关联式：

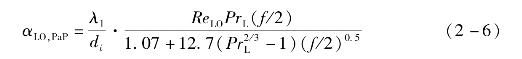
当0.5≤Pr L≤2 000且2 300≤Re LO≤104时，采用Gnielinski关联式：

式中，摩擦因子f为

对于混合工质，Kandlikar根据挥发性参数V l和沸腾数Bo分为3个区域：

（1）近共沸区：V l≤0.03，采用纯工质的关联式计算；

（2）中度扩散诱导的抑制区：当0.03＜V l＜0.2且Bo＞10-4时，换热系数主要由对流换热决定，采用Petukhov-Popov关联式；

（3）高度扩散诱导的抑制区：0.03＜V l＜0.2且Bo≤10-4，或者V l≥0.2，考虑大浓度差引起的质量扩散阻力，对对流传热式进行修正，引入扩散诱导的抑制因子FD：

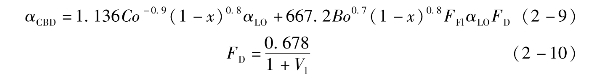
挥发性参数定义为

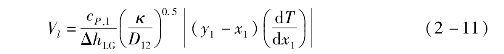
对于不锈钢直管，试验结果与采用传热关联式计算结果的对比表明二者之间存在一定的偏差，在同样的压力和温度下，试验结果比计算结果低46%～58%。因此，采用流体表面参数F Fl来修正结果。混合工质的F Fl计算式为

设定MM的流体表面参数为0.1，MDM的流体表面参数为0.8，在保持蒸发压力或蒸发器出口温度不变时，不同混合工质浓度比下采用式（2-12）修正以后的混合工质对流换热系数的计算结果与试验结果的对比如图2-4所示，二者的平均偏差仍然达到17%。仅采用高度扩散诱导的抑制区的传热关联式进行计算，发现计算结果与试验结果的偏差减小到10%。因此，在具体进行蒸发器面积估算时，需要对采用的传热关联式精度进行评估，减小工质与热源换热过程中的对流换热系数的估算偏差。采用Kandlikar关联式估算预热器和蒸发器面积时，采用混合工质后其换热面积比MM工质分别增大了0.9%和14%。

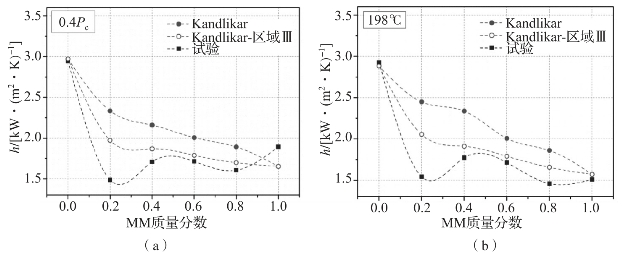
图2-4　对流换热系数的计算结果与试验结果的对比［2］

（a）工作压力等于0.4P c；（b）混合工质饱和气态温度等于198℃