计算有机工质热物性

有机朗肯循环采用有机物作为工质，可将低品位热源的热能转换为机械能输出。在进行ORC系统设计和性能计算时，有机工质热物性的计算至关重要。在进行ORC系统研究时，常常利用有机工质热物性计算软件，如美国国家标准与技术研究院（National Institute of Standards and Technology，NIST）的Refprop软件和F-Chart公司的EES软件等。这些软件采用基于赫姆霍兹自由能或吉布斯自由能的多参数状态方程来确定有机工质在不同压力和温度下的焓和熵等热物性。通常根据有机工质的T-s图中饱和蒸汽线的斜率将其分为干工质、等熵工质和湿工质。如图1-1所示，P点为工质的临界点，干工质的饱和气态特性线斜率大于零，等熵工质的饱和气态特性线近乎垂直，湿工质的饱和气态特性线斜率小于零。

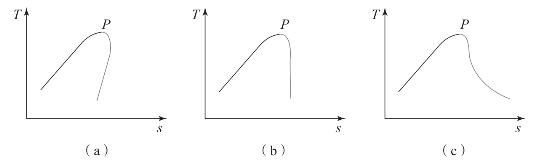
图1-1　有机工质的类型

（a）干工质；（b）等熵工质；（c）湿工质

为避免有机工质在膨胀过程中产生液击现象，有机朗肯循环常采用干工质或等熵工质。常见湿工质有：水、二氧化碳、氨、甲烷、乙烷、丙烷、四氟甲烷、甲醇和乙醇等。常见的干工质有：芳烃、丙醇及碳分子数更大的醇类，碳分子数比较大的氢氟烃如八氟丙烷，丁烷及碳分子数更大的烷烃。近似等熵工质有：异丙醇、R134a、R11和R12等。根据工质T-s图上饱和气态特性线的斜率可判断工质的干湿性，饱和气态特性线的走向与分子结构和蒸发焓等有很大关系［1］。

利用有机工质的状态方程可以判断有机工质的类型。有机工质熵的全微分可表示为

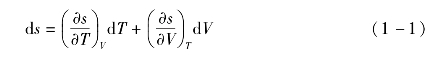
则沿着饱和气态特性线有

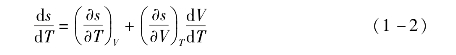
根据定容比热容cV的定义和麦克斯韦方程有

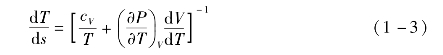
如果表示为s（T，P）的全微分，则有

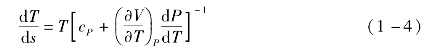
如果已知有机工质的状态方程，通过式（1-3）或式（1-4）可求得T-s图中饱和气态特性线的斜率，进而判断有机工质的干湿性［2］。

在低压下，有机工质接近理想气态，式（1-4）可简化为

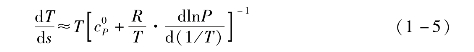
由于

代入式（1-5）可得

在已知有机工质的定压比热容和蒸发焓等热物性时，可利用式（1-7）对有机工质的干湿性进行估计。

在有机朗肯循环工作过程的T-s图中，有机工质的饱和气态特性线的精度对有机工质在膨胀机内的膨胀过程的计算精度有重要影响。整个过程的热力学性能与饱和气态特性线的斜率有很大的相关性。Garrido等提出了一种计算纯工质饱和气态特性线斜率的方法［2］。基于范德华型的立方状态方程，利用赫姆霍兹自由能可计算出关于温度的一阶和二阶微分量，进一步计算无量纲量ψ与定压比热容cP的差值，可判断工质的干湿性。一般来说，有机工质的分子中原子数目较少时为湿工质，随着原子数目的增加，逐渐变为干工质，且饱和气态特性线的斜率逐渐减小。

有机工质的吉布斯自由能G的微分可表示为

其中

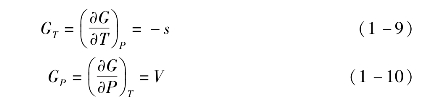
当有机工质处于饱和气态时，气态和液态吉布斯自由能的变化相等，有

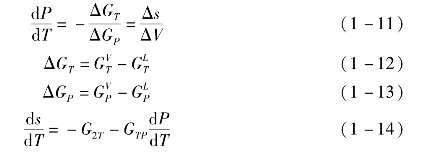
进一步求二阶导数有

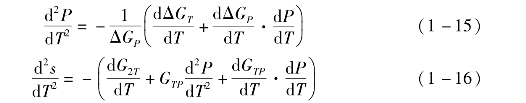
通常状态方程表示为T和V的函数，对上式进行勒让德变换后表示为赫姆霍兹自由能A的函数，可得到

其中

通过状态方程可求得赫姆霍兹自由能，从而可利用d s/d T来判断有机工质的类型。设流体的状态方程为范德瓦尔方程，可得到

其中，无量纲量ψ为

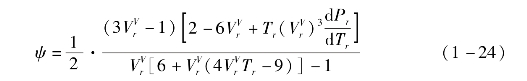
对纯工质，当其处于饱和气态时，Vr和Pr均可表示为Tr的函数。因此，ψ可表示为Tr的单值函数，如图1-2中实线ABCDE所示。在Tr=0.72处，ψ存在一个最小值。由于有机工质的理想气体定压比热容也仅为温度的函数，图1-2中也给出了甲烷、乙烷和丙烷的值，分别如图中虚线所示，根据式（1-23）可知甲烷和乙烷均为湿工质，而当Tr处于B点和D点之间时，丙烷为干工质。

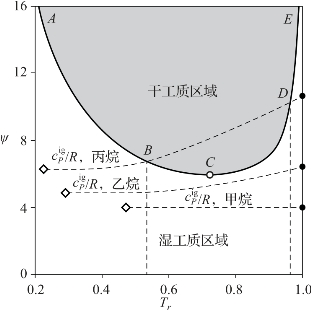
图1-2　纯工质类型的判定［2］

对采用混合工质的ORC系统，有机工质热物性的计算精度也是进行系统性能评估的基础。Refprop软件对混合工质热物性的计算是基于赫姆霍兹自由能进行的［3］。以温度、密度和组分质量分数组成的矢量x为自变量，混合工质的无量纲赫姆霍兹自由能可表示为

式中，δ为相对密度，τ为相对温度的倒数。

理想气体的无量纲赫姆霍兹自由能为

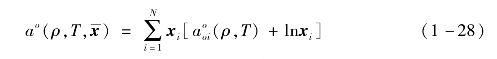
式中，为组分i的理想气态状态的无量纲赫姆霍兹自由能。

剩余赫姆霍兹自由能可表示为

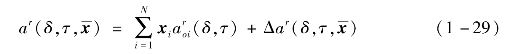
式中，为组分i的相对赫姆霍兹自由能的剩余部分，Δar为偏离函数。

在GERG-2008多参数状态方程中，采用下式计算剩余赫姆霍兹自由能［4］：

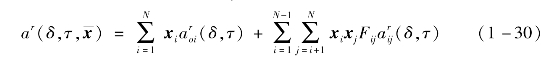
在式（1-28）中，组分i的理想气体状态无量纲赫姆霍兹自由能可由Jaeschke和Schley［5］的方程积分得到。

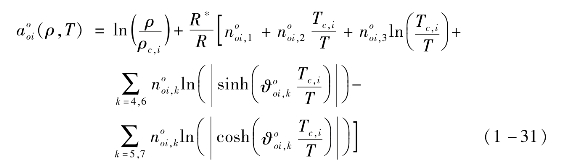
式中，和为拟合系数。

组分i的剩余赫姆霍兹自由能由下式计算：

式中，doi，k，toi，k，coi，k为拟合系数。

偏离函数项中（δ，τ）可表示为

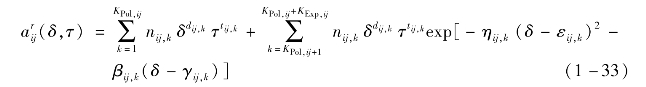
在求得相对赫姆霍兹自由能a后，其他热力学量也可相应求出。有机工质的压力可由下式计算：

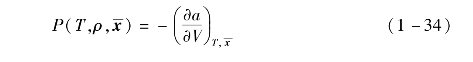
混合工质的熵为

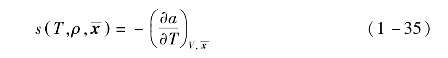
压缩因子为

内能为

比焓为

吉布斯自由能为

定容比热容和定压比热容分别为

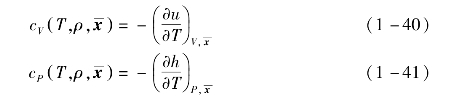
声速为

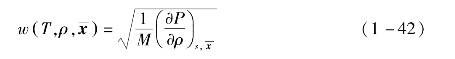
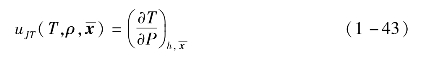
焦汤系数为等温节流系数为

(www.xing528.com)

绝热指数为

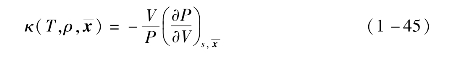
第二阶维里系数为

第三阶维里系数为

组分i的化学势为

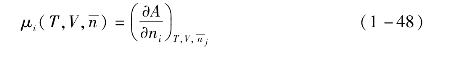
组分i的逸度系数为

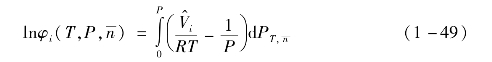
组分i的逸度为

根据以上公式，可计算出有机工质的各项热物理属性值。

对于混合工质而言，热物性计算中相对密度和相对温度与混合物的组分质量分数相关，在GERG-2008模型中，混合工质的临界密度ρr表示为

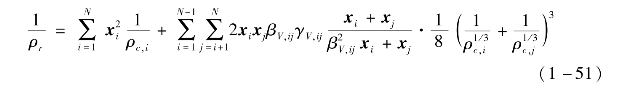
临界温度Tr的计算式为

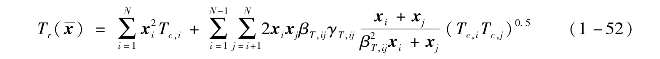
其中二元交互参数βV，ij，γV，ij，βT，ij，γT，ij需要根据混合工质的气液平衡ρx T试验数据进行拟合。Bell和Lemmon采用了基于随机优化算法的二元交互参数拟合方法［6］，获得了较好的拟合结果。Refprop 9.1软件中包含697组混合物的二元交互参数，其中有200组数据是从文献中获得的试验数据拟合的，但对某型新型有机工质可能不存在试验数据，而是采用某个类型的通用拟合系数，实际计算时可能会存在一定的误差［7］。

随着混合工质组分质量分数的变化，某些混合工质可能会出现由干工质到湿工质的转换。由于有机工质的干湿性对膨胀机的工作过程和整个循环的热力学性能有很大影响，为预测混合工质的干湿性，Albornoz等根据饱和气态特性线和热力学方程提出了一种理论计算方法［8］。该方法基于流体的状态方程，通过构建的无量纲量可判断有机工质的干湿性，并发现对于非共沸混合工质可能存在多次干湿性的转换现象。

当二元混合工质处于气液平衡时，每一种工质的化学势相等，有

式中，α、β分别为主相和邻相。

混合工质在气液平衡状态经过一个小扰动到达另一个平衡状态：

对二元混合工质的吉布斯自由能函数求微分，有

其中

另一方面，将吉布斯自由能对x微分，有

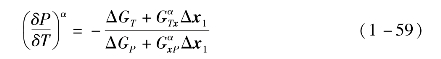
由式（1-56），对吉布斯自由能函数GT求二阶微分，有

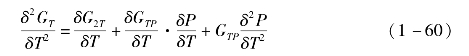
有机工质的吉布斯自由能可表示为理想吉布斯自由能与剩余吉布斯自由能的和，而理想吉布斯自由能可表示为

式中，G th等效于赫姆霍兹自由能的热贡献部分。由于吉布斯自由能可分为构型贡献和热贡献的和，则构型贡献部分的吉布斯自由能为

定义无量纲量ψ为

当混合工质为等熵工质时，有δs/δT=0，则根据式（1-63）可得

当时，为干工质；当时，为湿工质。

图1-3显示了甲烷与其他烷烃的二元混合工质的干湿性计算结果。甲烷为湿工质，而丁烷、戊烷、己烷和庚烷为干工质，当甲烷摩尔浓度很大时，混合工质为湿工质；当甲烷浓度较低时，混合工质为干工质。图中的点标示了不同混合工质干湿性转换的甲烷浓度值。

当多组分工质处于气液平衡状态时，组分的气态分数可由Rachford-Rice方程求得：

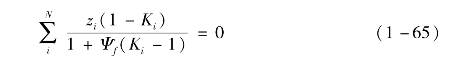
式中，Ψf为待求的组分气态分数，zi为组分i的摩尔浓度，Ki为组分i的平衡比。

基于活度系数法，平衡比可表示为

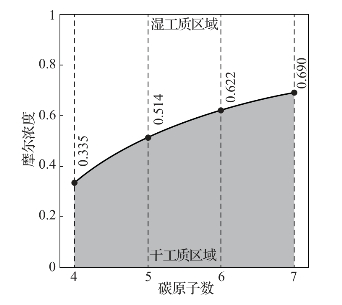
图1-3　混合工质干湿性的判定［8］

式中，γi为组分i的液相活度系数，为饱和蒸气压，为纯组分i在饱和压力下的逸度系数，为混合物逸度系数，VL，i为纯组分的摩尔体积。

活度系数采用UNIFAC模型计算，该方法基于基团贡献和UNIQUAC活度系数模型。活度系数分为考虑分子大小和表面积的组合项以及剩余项：

组合项计算式为

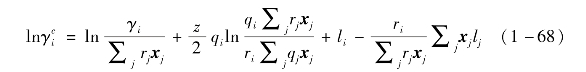
剩余项为

气态的逸度系数采用PSRK状态方程求解：

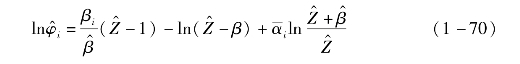
气态压缩因子可由下式求解，取最小的根：

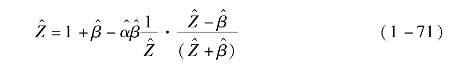
状态方程变量为

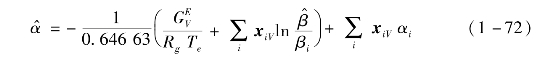
偏摩尔量可由式（1-72）求导得到。

饱和蒸气压由Riedel对比态公式求解：

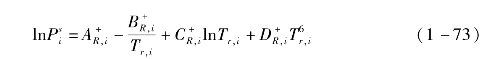
液体体积由Change和Zhao［9］提出的压缩液体体积关联式求解：

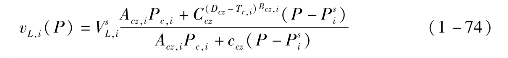
混合工质液态焓的计算式为

式中，为液态混合物的超额焓，可由活度系数求得。

气态焓的计算式为

式中，为组分i的剩余焓；为混合物的剩余焓，可根据状态方程求得；

为组分i的蒸发焓，可由Watson方程［10］求得。

液态熵的计算式为

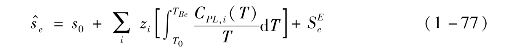
式中，为超额熵，可由超额焓和超额吉布斯自由能求得。

气态熵的计算式为

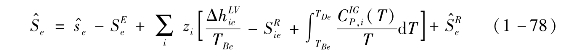
式中，组分i的剩余熵和混合物的剩余熵可由状态方程求得。