欧拉公式是在材料服从胡克定律条件下导出的,因此,压杆的临界应力不应超过材料的比例极限σp。欧拉公式的适用条件可表达为:

当σcr =σp 时,则有:
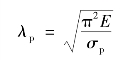
λp 就是某一种材料的细长压杆,用欧拉公式确定临界应力时的柔度最小值,称为极限柔度。所以,欧拉公式的适用范围用柔度表达的形式为:

式(12.8)是欧拉公式的适用范围的数学表达式。只有满足该式时,才能用欧拉公式计算压杆的临界力或临界应力。λmax >λp 的压杆称为大柔度杆,由此可知,欧拉公式只适用于较细长的大柔度杆。
λp 的大小与材料的力学性能有关,不同的材料的λp 值不同。例如Q235 钢,若取E =2.1 ×105 MPa,σp =200 MPa,其λp 则为:
![]()
这就是说,对于Q235 钢制成的压杆,只有当λ≥100 时才能运用欧拉公式;对于铸铁,λp 约为80;对于松木,λp 约为60。将临界应力公式中的σcr与λmax间的函数关系用曲线来表示,如图12.6 所示。图中的实线部分为欧拉公式适用范围的曲线,曲线的虚线部分因临界应力超过材料的比例极限,欧拉公式已不再适用,所以没有意义。
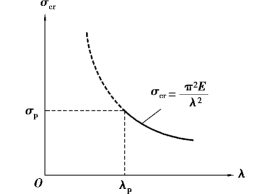
图12.6
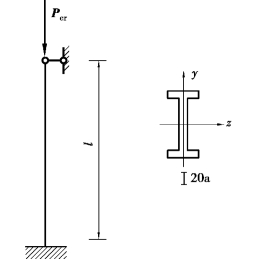
图12.7
【例12.2】 有一根长l=3.6 m 的压杆,截面为 20a 工字钢,一端固定,一端铰支,材料为Q235 钢,E=2 ×105 MPa,如图12.7 所示。试计算压杆的临界力和临界应力。(https://www.xing528.com)
【解】 ①计算λmax。压杆一端铰支,一端固定时,μ =0.7。Iy、Iz 为形心主惯性矩,Imin =Iy,压杆失稳则以y 轴为中性轴发生弯曲变形。查型钢表得:

压杆为细长杆,可用欧拉公式计算临界力。
②计算Pcr。
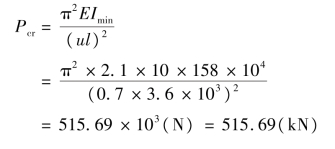
③计算σcr。
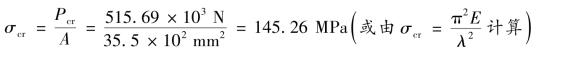
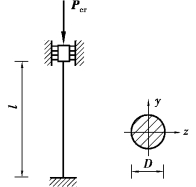
图12.8
【例12.3】 图12.8 为一压杆示意图,其两端支承情况为:上端定向支承,下端固定。已知杆为木材,l =3 m,D =60 mm,材料的弹性模量E=10 ×103 MPa,试计算该压杆的临界力。
【解】 先计算压杆长细比,判断是否为细长杆。
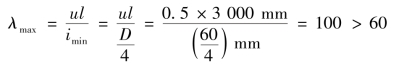
压杆是长细杆。
临界力为:
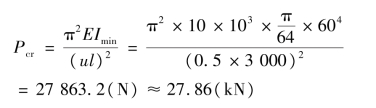
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




