临界力：欧拉公式解析

轴向受压杆受到轴向力的作用时,在干扰力作用下会发生弯曲变形。但其轴向力刚好等于临界力时,在干扰力撤除后其变形不会继续发展,会维持在初始变形时的位置。因此,我们可以根据其初始变形,即受临界力和干扰力时的变形形状推导出临界力的计算公式。

图12.4

首先考察如图12.4(a)所示两端铰支的轴向受压杆的变形,并根据其变形和变形边界条件写出变形方程:

上式为半个正弦波的表达式,其中y 为任一截面处挠度,f 为最大挠度。

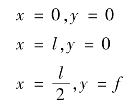
用截面法截取下部压杆作受力图,如图12.4(b),写出平衡方程:

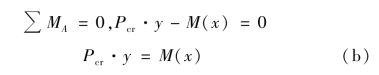
对于12.4 图受轴向压力产生的变形,从弯曲的角度来看,可以看作由弯矩M(x)引起的变形。根据第9 章弯矩变形的微分方程有:

将式(b)代入式(c)得:

再将式(a)代入式(d)并求二阶导数:

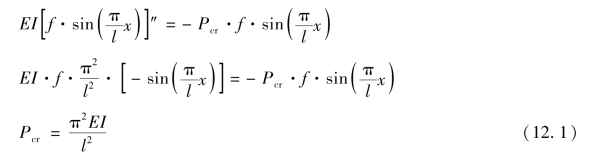
式(12.1)中的惯性矩I 由弯曲变形知,弯曲应首先发生在抗弯能力较弱的一方,所以应为Imin。再考察压杆两端在其他不同约束情况下的变形,分别根据变形和变形边界条件写出其半个正弦波长杆的变形方程,再二次求导得出各种情况下的临界力计算公式(推导略)。(www.xing528.com)

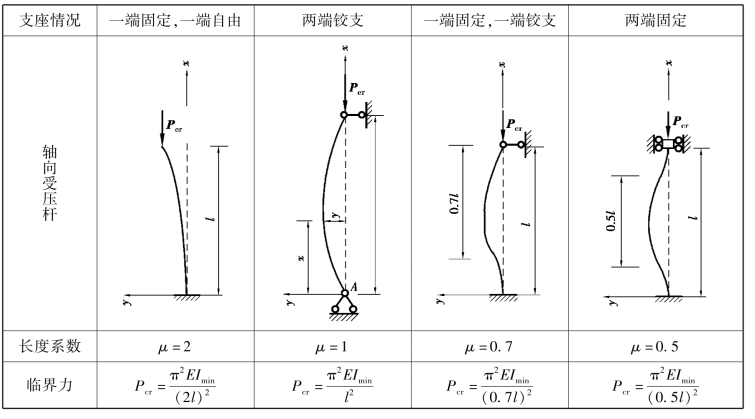
现将各种约束情况压杆变形波长图及临界力推导结果列于表12.1 中供查用。

从表12.1 中可知,各种约束临界力计算公式只是分母中l 前边的系数不同,临界力公式可写成下面统一形式:

式中,μl 称为计算长度,μ 称为长度系数。式(12.2)为欧拉公式,原推导用的是解常微分方程法,较难。

表12.1　不同支座压杆临界力

【例12.1】　一端固定、一端自由的细长轴心受压杆,长度l =1 m,弹性模量E =2.0 ×105 MPa,试分别计算图12.5(b)、(c)所示两种截面的临界力。

图12.5

【解】　已知杆为细长压杆。

①计算矩形截面。杆件在最小抗弯刚度平面内失稳。

②计算圆环截面。

例中两种截面的面积接近相等,但临界力相差很大。这是因为各截面形式不同,最小惯性矩差别很大所致。