求简支梁截面上任意点的正应力分布，及最小正应力点坐标

(1)任意截面应力

将力F 沿y 轴和z 轴分解为两个分量Fy 和Fz(这时的y 和z 代表的是方向),得:

这两个分量分别引起沿铅垂面和水平面的平面弯曲。求此情况下距自由端为x 的截面上任意点K 的正应力,该点的坐标为z 和y(这时的y 和z 代表的是位置)。

先求出x 截面的弯矩Mz 和My(这时的y 和z 代表的是中性轴):

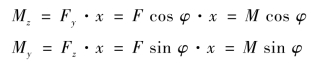
任一点K 的正应力可以应用第9 章中计算公式进行计算,设Mz 代表以z 为中性轴的弯曲,引起的应力设为σ′,My 代表以y 为中性轴的弯曲,引起的应力设为σ″,则有:

以z 轴为中性轴时的应力:

以y 轴为中性轴时的应力:

应力的正负号可以通过观察梁的变形来确定。拉应力取正号,压应力取负号。

应用叠加法,K 点的应力为:(www.xing528.com)

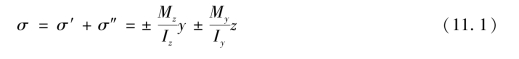
(2)危险截面应力

在做强度计算时,须先确定危险截面,然后在危险截面上确定危险点。对斜弯曲来说,与平面弯曲一样,通常也是由最大正应力控制。所以,对如图11.4 所示的悬臂梁来说,危险截面显然在固定端处,因为该处弯矩Mz 和My 的绝对值达到最大。至于要确定该截面上的危险点的位置,则对于工程中常用的具有凸角而又有两条对称轴的截面,如矩形、工字形等,根据对变形的判断,可知最大正应力发生在ID 与ED 相交的D 点。

最小正应力发生IH 与HE 的相交的H 点。

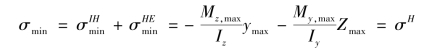
(3)强度计算公式

若材料的抗拉与抗压强度相同,其强度条件就可以写为:

式中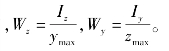

对于不易确定危险点的截面,如边界没有棱角而呈弧线的截面,如图11.5 所示,则需要研究应力的分布规律,确定中性轴位置。为此,将斜弯曲正应力表达式改写为:

式(11.3)表明,发生斜弯曲时,截面上的正应力是y 和z 的线性函数,所以它的分布规律是一个平面,如图11.6 所示某简支梁截面应力情况。此应力平面与y、z 坐标平面(即x 截面)相交于一直线,在此直线上应力均等于零。所以,该直线为中性轴。