利用应力圆可以分析单元体上任意斜截面上的应力,尤其是可以方便地确定单元体上应力的极值及其作用面的方位。正应力的极值称为主应力,主应力的作用面称为主平面。下面就由应力圆给出计算单元体的主应力、主平面位置及最大剪应力的计算式。
(1)主应力
由图10.10(b)可见,在应力圆的横坐标轴上A1、A2 两点的正应力是σmax和σmin,这两点的纵坐标都等于零,即表示单元体上对应的截面上剪应力 =0。因此,A1、A2 两点的正应力就是两个主应力。
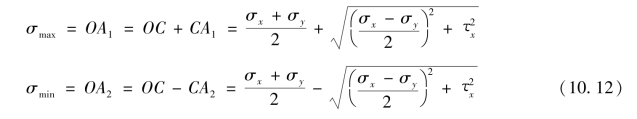
(2)主平面的方位
圆上D1 点到A1 点为顺时针转旋转2α0,在单元体上由x 轴按顺时针旋转α0 便可确定主平面的法线位置。顺时针旋转的角度为负角,从应力圆上可得主平面的位置为:
应力圆上从A1 点到A2 点旋转了180° [图10.10(b)],单元体上相应面的夹角为90°,说明两个主平面相互垂直。两个主平面上的主应力,一个是极大值,用σmax或σ1 表示;另一个是极小值,用σmin或σ2 表示[图10.10(c)]。σ1 沿着单元体上剪应力 所指的象限。一般情况下,平面应力状态有3 个互相垂直的主平面(其中一个主平面与纸平面平行)和3 个主应力(有一个主应力等于零)。3 个主应力通常用σ1、σ2、σ3 表示,并按代数值的大小排列,即σ1≥σ2≥σ3。
(3)最大剪应力及其平面的方位
在如图10.10(b)所示应力圆上的F1 点、F2 点处,有最大剪应力和最小剪应力。
从A1 点到F1 点旋转了90°,单元体上相应面的夹角为45°,这说明单元体中的最大剪应力所在平面与主平面相差45°。
式(10.14)表明,剪应力的极值等于两个主应力差的1/2。(www.xing528.com)
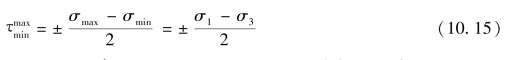
【例10.2】 求如图10.11(a)所示一单元体的主应力与主平面,并求最大剪应力。已知σx =20 MPa,σy = -10 MPa, x =20 MPa。
图10. 11
【解】 ①确定单元体的主平面,由式(10.13),得:
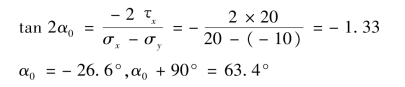
②计算主应力,由式(10.12),得:
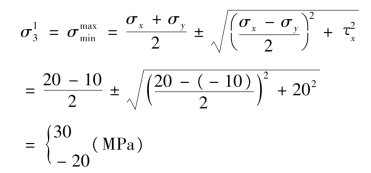
由此,3 个主应力分别为:
单元体如图10.11(b)所示,最大主应力σ1 偏向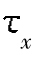
指向的一侧。
③最大剪应力可由式(10.15)直接得出:
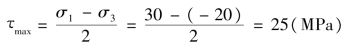
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
