梁上各点应力分析

如图10.2 所示,现拿一根在荷载作用下的梁在某截面产生正剪力V 和正弯矩M 的情况进行讨论。梁的最下边缘点即⑤点只受拉应力作用,剪应力等于零,故属于单向应力状态;梁的上边缘点即①点只受压应力作用,剪应力等于零,也属于单向应力状态;③点只受剪应力作用,属于纯剪状态,而②点和④点既有正应力又有剪应力,属于平面应力状态。

1)特殊点斜截面上的应力

①点、⑤点和③点都是梁上的特殊点,其中①点与⑤点类似,只需要研究⑤点斜截面上的应力。设有一与梁轴线成α 角的斜截面截开⑤点,求⑤点上沿斜截面方向上的应力。

图10.2

取⑤点单元体进行分析,α 斜截面的应力有正应力σα 和剪应力 α,如图10.3 所示。列平衡方程求σα 和 α,现用斜截面BC 将单元体切开(图10.3),斜截面的外法线n 与x 轴的夹角用α 表示(以后BC 截面称为α 截面),在α 截面上的应力用σα 及 α表示。规定α 角由x 轴到n轴逆时针转向为正;正应力σα 以拉应力为正;压应力为负;剪应力 α以对单元体顺时针转向为正,反之为负。

取BC 左部分为研究对象[图10.3(c)],设斜截面上的面积为dA,则BA 面和AC 面的面积分别为dA cos α 和dA sin α。建立坐标如图10.3(d)所示,取n 和t 为两参考坐标轴,列出平衡方程分别为:

图10.3

由式(10.1)、式(10.2)可见,同样,①点斜截面上有正应力和剪应力,它们的大小随截面的方位α 角的变化而变化。

当α=0°时,正应力达到最大值:

由此可见,梁上下边缘的最大正应力发生在横截面上。

取③点单元体进分析,α 斜截面的应力有正应力σα 和剪应力 α,如图10.4 所示,列平衡方程求σα 和 α:

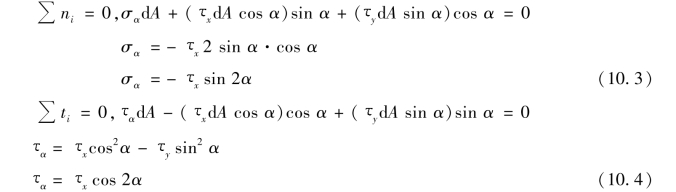(www.xing528.com)

由式(10.3)、式(10.4)可见,③点斜截面上有正应力和剪应力,它们的大小随截面的方位α 角的变化而变化。

当α=0°时,剪应力达到最大值:

由此可见,最大剪应力发生梁中横截面上。

当时α=45°时,正应力绝对值达到最大值:

图10.4

2)一般点斜截面上的应力

如图10.2 所示,④点和②点为一般点,②点与④点类似,只需分析④点应力。其实④点的应力情况等于⑤点和③点应力的叠加。

式(10.5)和式(10.6)是计算平面应力状态下任一斜截面上应力的一般公式。

【例10.1】　单元体各面应力如图10.5 所示,试求α=30°斜截面上的应力σα、 α。

【解】　已知σx =30 MPa, x = -20 MPa。

图10.5