梁横截面剪应力优化分析

1)剪应力分布规律假设

对于高度h 大于宽度b 的矩形截面梁,其横截面上的剪力V 沿y 轴方向,如图9.33(a)所示。现假设剪应力的分布规律如下:

①横截面上各点处的剪应力 都与剪力V 方向一致;

②横截面上距中性轴等距离各点处剪应力大小相等,即沿截面宽度为均匀分布。

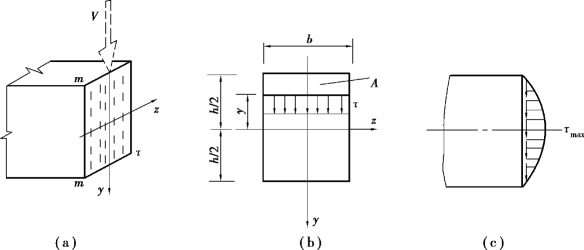
图9.33

2)矩形截面梁的剪应力计算公式

根据以上假设,可以推导(略)出矩形截面梁横截面上任意一点处剪应力的计算公式为:

式中　V——横截面上的剪力;

Iz——整个截面对中性轴的惯性矩;

b——需求剪应力处的横截面宽度;

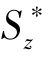——横截面上需求剪应力点处的水平线以上(或以下)部分的面积A∗对中性轴的静矩。

用式(9.5)计算时,V 与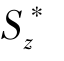均用绝对值代入即可。

剪应力沿截面高度的分布规律,可从式(9.5)得出。对于同一截面,V、Iz 及b 都为常量。因此,截面上的剪应力 随静矩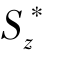的变化而变化。

现求图9.33(b)所示矩形截面上任意一点的剪应力,该点至中性轴的距离为y。该点水平线以上横截面面积A∗对中性轴的静矩为:

又有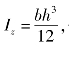代入式(9.5)得:

上式表明,剪应力沿截面高度按二次抛物线规律分布[图9. 33(c)]。在上、下边缘处剪应力为零;在中性轴上(y=0),剪应力最大,其值为:

式中　——截面上的平均剪应力。(www.xing528.com)

由此可见,矩形截面梁横截面上的最大剪应力是平均剪应力的1.5 倍,发生在中性轴上。

3)工字形截面梁的剪应力

工字形截面梁由腹板和翼缘板组成[图9.34(a)]。腹板是一个狭长的矩形,所以它的剪应力可按矩形截面的剪应力公式计算。

式中　d——腹板的宽度;

——横截面上所求剪应力处的水平线以下(或以上)至边缘部分面积对中性轴的静矩。

由式(9.7)可求得剪应力 沿腹板高度按抛物线规律变化,如图9.34(b)所示。最大剪应力发生在中性轴上,其值为:

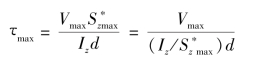
式中　——工字形截面中性轴以下(或以上)面积对中性轴的静矩。对于工字钢,可由附录中查得。

翼缘板部分的剪应力很小,一般情况不必计算。

图9.34

【例9.17】　一矩形截面简支梁如图9.35 所示。已知l=3 m,h=160 mm,b=100 mm,h1 =40 mm,F=3 kN,求m—m 截面上K 点的剪应力。

图9.35

【解】　①求支座反力及m—m 截面上的剪力。

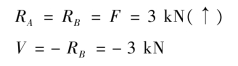
②计算截面的惯性矩及面积A∗对中性轴的静矩分别为:

③计算m—m 截面上K 点的剪应力: