梁横截面的正应力分布特点

1)正应力分布规律

为了解正应力在横截面上的分布情况,可先观察梁的变形,取一弹性较好的矩形截面梁,在其表面上画上一系列与轴线平行的纵向线及与轴线垂直的横向线,构成许多均等的小矩形,然后在梁的两端施加一对力偶矩为M 的外力偶,使梁发生纯弯曲变形,如图9.29 所示。这时可观察到下列现象:

①各横向线仍为直线,只倾斜了一个角度。

②各纵向线弯成曲线,上部纵向线缩短,下部纵向线伸长。

图9.29

根据上面所观察到的现象,推测梁的内部变形,可作出如下的假设和推断:

①平面假设。各横向线代表横截面,变形前后都是直线,表明横截面变形后仍保持平面,且仍垂直于弯曲后的梁轴线。

②单向受力假设。将梁看成由无数层纤维组成,每层又由无数根纤维组成,各纤维只受到轴向拉伸或压缩,不存在相互挤压。

从上部各层纤维缩短到下部各层纤维伸长的连续变化中,必有一层纤维既不缩短也不伸长,这层纤维称为中性层。中性层与横截面的交线称为中性轴,如图9.29(c)所示。中性轴通过横截面形心,且与竖向对称轴y 垂直,并将梁横截面分为受压和受拉两个区域。由此可知,梁弯曲变形时,各截面绕中性轴转动,使梁内纵向纤维伸长或缩短,中性层上纵向各根纤维的长度不变。通过进一步的分析可知,各层纵向纤维的线应变沿截面高度应为线性变化规律,而从由胡克定律可推出,梁弯曲时横截面上的正应力沿截面高度呈线性分布规律变化,如图9.30 所示。

2)矩形截面正应力计算公式

公式推导示意如图9.30、图9.31 所示。

图9.30

图9.31

中性轴以下应力形成的合力为R,与中性轴以上应力形成的合力R′。

截面上应力形成总弯矩为:

由式(b)得:

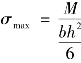(www.xing528.com)

由图9.30 正应力分布情况知:

又令

将式(d)代入式(c)得梁弯曲时矩形横截面上任一点正应力的计算公式为:

式中　M——横截面上的弯矩;

y——所计算应力点到中性轴的距离;

Iz——截面对中性轴的惯性矩。

式(9.4)说明,梁弯曲时横截面上任一点的正应力σ 与弯矩M 和该点到中性轴距离y 成正比,与截面对中性轴的惯性矩Iz 成反比,正应力沿截面高度呈线性分布;中性轴上(y =0)各点处的正应力为零;在上、下边缘处(y=ymax)正应力的绝对值最大。用式(9.4)计算正应力时,M和y 均用绝对值代入。当截面上有正弯矩时,中性轴以下部分为拉应力,以上部分为压应力;当截面有负弯矩时,则相反。

其他截面正应力计算公式与矩形截面相同,推导从略。

【例9.16】　长为l 的矩形截面悬臂梁,在自由端处作用一集中力F,如图9.32 所示。已知F=3 kN,h=180 mm,b=120 mm,y=60 mm,l=3 m,a=2 m,求C 截面上K 点的正应力。

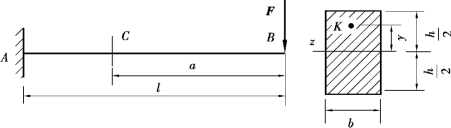
图9.32

【解】　①计算C 截面的弯矩。

②计算截面对中性轴的惯性矩。

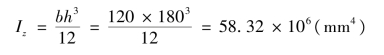
③计算C 截面上K 点的正应力。将MC、y(均取绝对值)及Iz 代入式(9.4),得:

由于C 截面的弯矩为负,K 点位于中性轴上方,所以K 点的应力为拉应力。