微分关系法绘制剪力图和弯矩图

利用弯矩、剪力与荷载集度之间的微分关系及其几何意义,可总结出下列一些规律,以用来校核或绘制梁的剪力图和弯矩图。

1)在无荷载梁段,即q(x) =0

由式(9.1)可知,V(x)是常数,即剪力图是一条平行于x 轴的直线;又由式(9.2)可知,该段弯矩图上各点切线的斜率为常数,因此,弯矩图是一条斜直线。

2)均布荷载梁段,即q(x) =常数

由式(9.1)可知,剪力图上各点切线的斜率为常数,即V(x)是x 的一次函数,剪力图是一条斜直线;又由式(9.2)可知,该段弯矩图上各点切线的斜率为x 的一次函数,因此,M(x)是x 的二次函数,即弯矩图为二次抛物线。这时可能出现两种情况,如图9.19 所示。

图9.19

3)弯矩的极值

由=V(x) =0 可知,在V(x) =0 的截面处,M(x)具有极值。即剪力等于零的截面上,弯矩具有极值;反之,弯矩具有极值的截面上,剪力一定等于零。

利用上述荷载、剪力和弯矩之间的微分关系及规律,可更简便地绘制梁的剪力图和弯矩图,其步骤如下:

①分段,即根据梁上外力及支承等情况将梁分成若干段;

②根据各段梁上的荷载情况,判断其剪力图和弯矩图的大致形状;

③利用计算内力的简便方法,直接求出若干控制截面上的V 值和M 值;

④逐段直接绘出梁的V 图和M 图。

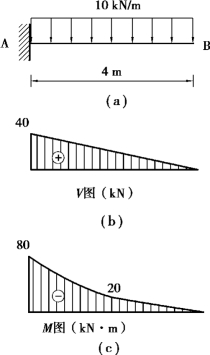
图9.20

【例9.9】　利用微分关系绘制如图9.20(a)所示悬臂梁的V 图和M 图。

【解】　①对于悬臂梁从自由端开始画图,可不求支座反力,根据梁的外力情况可知梁仅为一段。

②计算控制截面剪力,画剪力图。

画出剪力图,如9.20(b)所示。

③计算控制截面弯矩,画弯矩图。因梁上作用有均布荷载,故该段梁的弯矩图为二次抛物线。因q 向下(q <0),所以曲线向下凸,因上侧受拉,所以弯矩图均画于基线以上,其控制截面弯矩为:

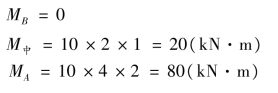
画出弯矩图,如图9.20(c)所示。

【例9.10】　试求作图9.21(a)所示外伸梁在集中力偶作用下的内力图。

图9.21

【解】　①求支座反力。

②根据梁上的外力情况将梁分段,将梁分为AB 和BC 两段。

③计算控制截面剪力,画剪力图。

BC 段:取B 右截面至C 段为研究对象,无竖向荷载作用,为无剪力区。

AB 段:为无荷载区段,剪力图为水平线,其控制截面剪力为:

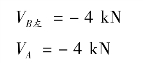
画出剪力图,如图9.20(b)所示。

④计算控制截面弯矩,画弯矩图。BC 段:取B 右截面到C 段为研究对象,由集中力偶作用可知, BC 段弯矩图为水平直线,其控制截面弯矩为:

AB 段:为无荷载区段,弯矩图为斜直线,其控制截面弯矩为:

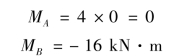
画出弯矩图,如图9.21(c)所示。

⑤请读者思考图9.21(d)的内力图。(www.xing528.com)

【例9.11】　一外伸梁,梁上荷载如图9.22(a)所示,已知l =4 m,利用微分关系绘出外伸梁的剪力图和弯矩图。

【解】　①求支座反力。

②根据梁上的外力情况将梁分段,将梁分为AB、BC 和CD 3 段。

③计算控制截面剪力,画剪力图。AB 段梁上有均布荷载,该段梁的剪力图为斜直线,其控制截面剪力为:

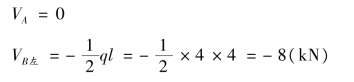
BC 和CD 段均为无荷载区段,剪力图均为水平线,其控制截面剪力为:

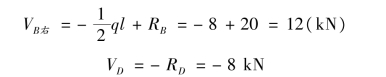
画出剪力图,如图9.22(b)所示。

④计算控制截面弯矩,画弯矩图。AB 段梁上有均布荷载,该段梁的弯矩图为二次抛物线。因q 向下(q<0),所以曲线向下凸,其控制截面弯矩为:

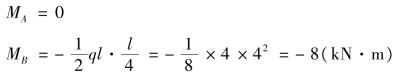
BC 段与CD 段均为无荷载区段,弯矩图均为斜直线,其控制截面弯矩为:

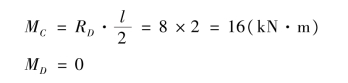
画出弯矩图,如图9.22(c)所示。

从以上看到,对本题来说,只需算出VB左、VB右、VD 和MB、MC,就可画出梁的剪力图和弯矩图。

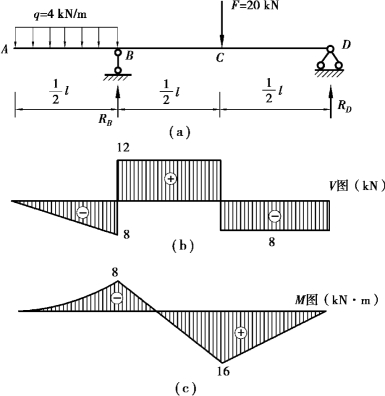
图9.22

【例9.12】　一简支梁的尺寸及梁上荷载如图9.23(a)所示,利用微分关系绘出此梁的剪力图和弯矩图。

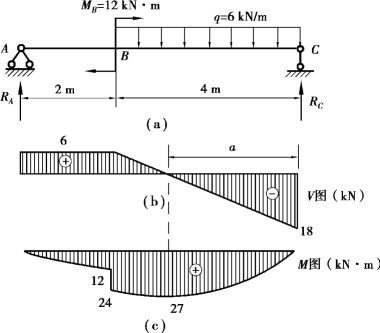
图9.23

【解】　①求支座反力。

②根据梁上的荷载情况,将梁分为AB 和BC 两段,逐段画出内力图。

③计算控制截面剪力,画剪力图。AB 段为无荷载区段,剪力图为水平线,其控制截面剪力为:

BC 为均布荷载段,剪力图为斜直线,其控制截面剪力为:

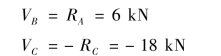
画出剪力图,如图9.23(b)所示。

④计算控制截面弯矩,画弯矩图。AB 段为无荷载区段,弯矩图为斜直线,其控制截面弯矩为:

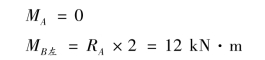
BC 为均布荷载段,由于q 向下,弯矩图为凸向下的二次抛物线,其控制截面弯矩为:

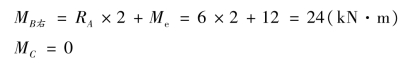
从剪力图可知,此段弯矩图中存在着极值,应该求出极值所在的截面位置及其大小。设弯矩具有极值的截面距右端的距离为a,由该截面上剪力等于零的条件可求得a 值。

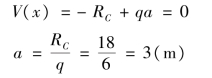
弯矩的极值为:

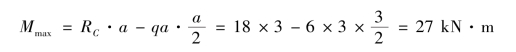
画出弯矩图,如图9.23(c)所示。

对本题来说,反力RA、RC 求出后,便可直接画出剪力图。而弯矩图,也只需确定MB左、MB右及Mmax值,便可画出。

在熟练掌握简便方法求内力的情况下,可以直接根据梁上的荷载及支座反力画出内力图。