剪力图和弯矩图简介

为了形象地表示剪力和弯矩沿梁轴线的变化规律,可以根据剪力方程和弯矩方程分别绘制剪力图和弯矩图。以沿梁轴线的横坐标x 表示梁横截面的位置,以纵坐标表示相应横截面上的剪力或弯矩。在工程中,习惯上把正剪力画在x 轴上方,负剪力画在x 轴下方;而把弯矩图画在梁受拉的一侧,即正弯矩画在x 轴下方,负弯矩画在x 轴上方,如图9.13 所示。

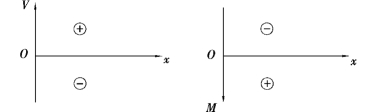
图9.13　画剪力图和弯矩图的规定

【例9.5】　悬臂梁受集中荷载作用如图9.14(a)所示,试画出梁的剪力图和弯矩图。

【解】　①建立坐标系。将坐标原点放在自由端A 点,列方程时就用不到支座反力,所以不用求支反力。

②列剪力方程和弯矩方程。取距A 点为x 处的任意截面,将梁假想截开,考虑左段平衡,可得:

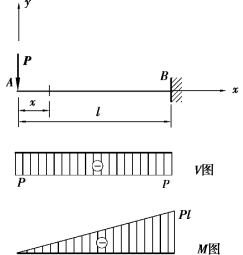
图9.14

③画剪力图和弯矩图。由式(1)可见,V(x)与x 无关,是一常量,剪力图是一条水平直线。

x=0 时,VA = -P。

x=l 时,VB = -P。

根据这两个截面的剪力值,画出剪力图,如图9.14(b)所示。

由式(2)知,M(x)是x 的一次函数,说明弯矩图是一条直线,与x 有关,应至少计算两个截面的弯矩值,才可描绘出直线形状。

x=0 时,MA =0。

x=l 时,MB = -Pl。

根据以上计算结果,画出弯矩图,如图9.14(c)所示。

从剪力图和弯矩图中可知,受集中荷载作用的悬臂梁,其剪力图为水平直线,弯矩图为斜直线,最大弯矩发生在固定端,其绝对值为

结论:在集中荷载作用的梁段,剪力图为水平直线,弯矩图为一斜直线。固定端弯矩绝对值最大。

【例9.6】　简支梁受均布荷载作用如图9.15(a)所示,试画出梁的剪力图和弯矩图。

【解】　①求支座反力。简支梁无论是从左端取分离体还是从右端取,都要先知道支座反力,因对称关系,可得:

②列剪力方程和弯矩方程。取距A 点为x 处的任意截面,将梁假想截开,考虑左段平衡,可得:

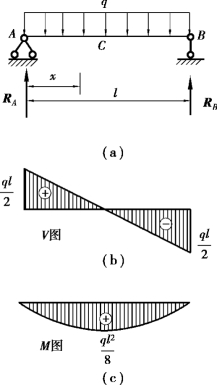
图9.15

③画剪力图和弯矩图。由式(1)可见,V(x)是x 的一次函数,即剪力方程为一直线方程,剪力图是一条斜直线。

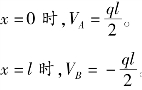
根据这两个截面的剪力值,画出剪力图,如图9. 15(b)所示。

由式(2)知,M(x)是x 的二次函数,说明弯矩图是一条二次抛物线,应至少计算3 个截面的弯矩值,才可描绘出曲线的大致形状。

根据以上计算结果,画出弯矩图,如图9.15(c)所示。

从剪力图和弯矩图中可知,受均布荷载作用的简支梁,其剪力图为斜直线,弯矩图为二次抛物线;最大剪力发生在两端支座处,绝对值为而最大弯矩发生在剪力为零的跨中截面上,其绝对值为

结论:均布荷载作用的梁段,剪力图为斜直线,弯矩图为二次抛物线。在剪力等于零的截面上弯矩有极值。

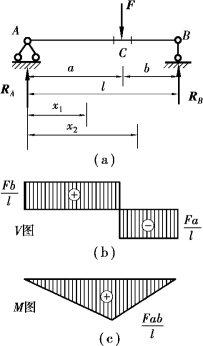
图9.16

【例9.7】　简支梁受集中力作用如图9.16(a)所示,试画出梁的剪力图和弯矩图。

【解】　①求支座反力。由梁的整体平衡条件,得:

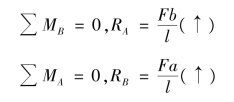
校核:(www.xing528.com)

计算无误。

②列剪力方程和弯矩方程。梁在C 处有集中力作用,故AC段和CB 段的剪力方程和弯矩方程不相同,要分段列出。

AC 段:距A 端为x1的任意截面处将梁假想截开,并考虑左段梁平衡,列出剪力方程和弯矩方程为:

CB 段:距A 端为x2 的任意截面处假想截开,并考虑左段的平衡,列出剪力方程和弯矩方程为:

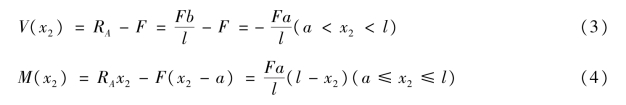
③画剪力图和弯矩图。根据剪力方程和弯矩方程画剪力图和弯矩图。

V 图:AC 段剪力方程V(x1)为常数,其剪力值为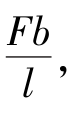剪力图是一条平行于x 轴的直线,且在x 轴上方。在x 轴下方。画出全梁的剪力图,如图9.16(b)所示。

CB 段剪力方程V(x2)也为常数,其剪力值为,剪力图也是一条平行于x 轴的直线,但

M 图:AC 段弯矩方程M(x1)是x1 的一次函数,弯矩图是一条斜直线,只要计算两个截面的弯矩值,就可以画出弯矩图。

根据计算结果,可画出AC 段弯矩图。

CB 段弯矩方程M(x2)也是x2的一次函数,弯矩图仍是一条斜直线。

x2 =l 时,MB =0。

由上面两个弯矩值,画出CB 段弯矩图。整梁的弯矩图如图9.16(c)所示。

从剪力图和弯矩图中可见,简支梁受集中荷载作用,当a>b 时,发生在BC 段的任意截面上;发生在集中力作用处的截面上。若集中力作用在梁的跨中,则最大弯矩发生在梁的跨中截面上,其值为

结论:在无荷载梁段,剪力图为平行线,弯矩图为斜直线。在集中力作用处,左右截面上的剪力发生突变,其突变值等于该集中力的大小,突变方向与该集中力的方向一致;而弯矩图出现转折,即出现尖点,尖点方向与该集中力方向一致。

【例9.8】　如图9.17(a)所示,简支梁受集中力偶作用,试画出梁的剪力图和弯矩图。

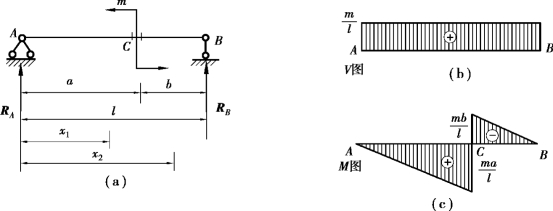
图9.17

【解】　①求支座反力。由整梁平衡,得:

校核:

计算无误。

②列剪力方程和弯矩方程。在梁的C 截面处有集中力偶m 作用,分两段列出剪力方程和弯矩方程。

AC 段:距A 端为x1 的截面处假想将梁截开,考虑左段梁平衡,列出剪力方程和弯矩方程为:

CB 段:在A 端为x2 的截面处假想将梁截开,考虑左段梁平衡,列出剪力方程和弯矩方程为:

③画剪力图和弯矩图。

V 图:由式(1)、(3)可知,梁在AC 段和CB 段剪力都是常数,其值为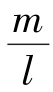,故剪力是一条在x轴上方且平行于x 轴的直线。画出剪力图,如图9.17(b)所示。

M 图:由式(2)、(4)可知,梁在AC 段和CB 段内弯矩方程都是x 的一次函数,故弯矩图是两段斜直线。

画出弯矩图,如图9.17(c)所示。

由内力图可见,简支梁只受一个力偶作用时,剪力图为一条平行线,而弯矩图是两段平行的斜直线,在集中力偶处左右截面上的弯矩发生了突变。

结论:梁在集中力偶作用处,左右截面上的剪力无变化,而弯矩出现突变,其突变值等于该集中力偶矩。