【摘要】:此规律着重从变形情况判断正负,可记为“翘上去、弯矩正”。利用上述规律直接由外力求梁内力的方法称为简易法。用简易法求内力可以省去画受力图和列平衡方程,从而简化计算过程。①求支座反力。由1—1 截面以左部分的外力来计算内力,根据“外力顺、剪力正”和“翘上去、弯矩正”得:图9.11图9.12用简易法求图9.12 所示悬臂梁C左和B左截面上的剪力和弯矩。
通过上述例题,可以总结出直接根据外力计算梁内力的规律。
1)求剪力的规律
计算剪力是对截面左(或右)段梁建立投影方程,经过移项后可得:
![]()
上两式说明:梁内任一横截面上的剪力在数值上等于该截面一侧所有外力在垂直于轴线方向投影的代数和。无论是取左段还是右段,外力对所求截面产生顺时针方向转动趋势时,引起的剪力刚好为正号[图9.7(a)];反之,为负号[图9.7(b)]。由此得出规律可记为“外力顺、剪力正”。
2)求弯矩的规律
计算弯矩是对截面左(或右)段梁建立力矩方程,经过移项后可得:
![]()
上两式说明:梁内任一横截面上的弯矩在数值上等于该截面一侧所有外力(包括力偶)对该截面形心力矩的代数和。将所求截面固定,若外力矩使所考虑的梁段产生下凸弯曲变形时(即上部受压,下部受拉),等式右边取正号[图9.8(a)];反之,取负号[图9.8(b)]。此规律着重从变形情况判断正负,可记为“翘上去、弯矩正”。
利用上述规律直接由外力求梁内力的方法称为简易法。用简易法求内力可以省去画受力图和列平衡方程,从而简化计算过程。现举例说明。
【例9.3】 用简易法求图9.11 所示简支梁1—1 截面上的剪力和弯矩。
【解】 ①求支座反力。由梁的整体平衡求得:
![]() (https://www.xing528.com)
(https://www.xing528.com)
②计算1—1 截面上的内力。由1—1 截面以左部分的外力来计算内力,根据“外力顺、剪力正”和“翘上去、弯矩正”得:
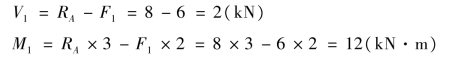
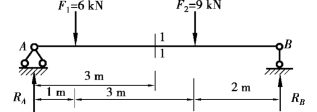
图9.11
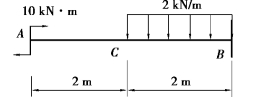
图9.12
【例9.4】 用简易法求图9.12 所示悬臂梁C左和B左截面上的剪力和弯矩。
【解】 因是悬臂梁,分离体取左段,故可以不求支座反力。
C左截面:
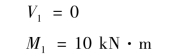
B右截面:
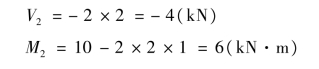
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




