使用截面法计算结构内力

1)剪力和弯矩

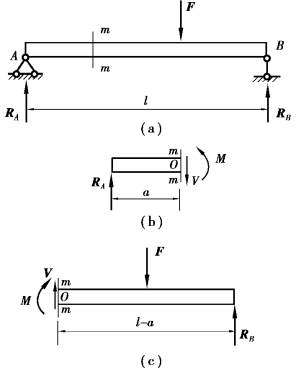
图9.6

图9.6(a) 所示为一简支梁,荷载F 和支座反力RA、RB 是作用在梁的纵向对称平面内的平衡力系。现用截面法分析任一截面m—m 上的内力。假想将梁沿m—m 截面分为两段,现取左段为研究对象。从图9.6(b) 可见,因有支座反力RA 作用,为使左段满足∑Y = 0,截面m—m 上必然有与RA 等值、平行且反向的内力V 存在,这个内力V 称为剪力;同时,因RA对截面m—m 的形心O 点有一个力矩RAa 的作用,为满足∑MO = 0,截面m—m 上也必然有一个与力矩RAa 大小相等且转向相反的内力偶矩M 存在,这个内力偶矩M 称为弯矩。由此可见,梁发生弯曲时,横截面上同时存在着两个内力素,即剪力和弯矩。

剪力的常用单位为N 或kN,弯矩的常用单位为N·m 或kN·m。剪力和弯矩的大小可由左段梁的静力平衡方程求得:

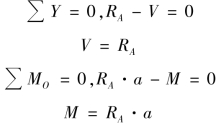
如果取右段梁作为研究对象,同样可求得截面m—m 上的V 和M。根据作用与反作用力的关系,它们与从左段梁求出m—m 截面上的V 和M 大小相等,方向相反,如图9.6(c)所示。

2)剪力和弯矩的正、负号规定

为了使从左、右两段梁求得同一截面上的剪力V 和弯矩M 具有相同的正负号,并考虑到工程上的习惯要求,对剪力和弯矩的正负号特作如下规定:

①剪力的正负号: 使梁段有顺时针转动趋势的剪力为正[图9.7(a)];反之,为负[图9.7(b)]。

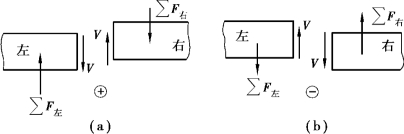
图9.7

②弯矩的正负号: 使梁段产生下凸变形或下侧受拉的弯矩为正[图9.8(a)];反之,为负[图9.8(b)]。

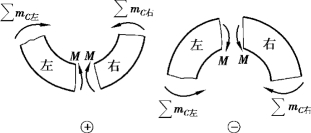
图9.8

3)用截面法计算指定截面上的剪力和弯矩

用截面法求指定截面上的剪力和弯矩的步骤如下:

①计算支座反力;

②用假想的截面在需求内力处将梁截成两段,取其中任一段为研究对象;

③画出研究对象的受力图(截面上的V 和M 都先假设为正的方向);

④建立平衡方程,解出内力。

下面举例说明用截面法计算指定截面上的剪力和弯矩。

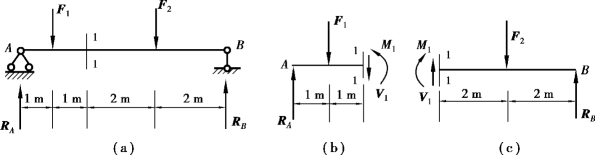
【例9.1】　如图9.9(a)所示简支梁,已知F1 =30 kN,F2 =30 kN,试求截面1—1 上的剪力和弯矩。

(www.xing528.com)

图9.9

【解】　①求支座反力,考虑梁的整体平衡,得:

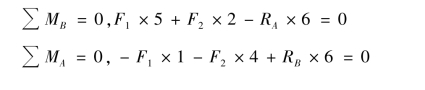
解得:

校核:

②求1—1 截面上的内力。在截面1—1 处将梁截开,取左段梁为研究对象,画出其受力,内力V1 和M1 均先假设为正的方向[图9.9(b)],列平衡方程:

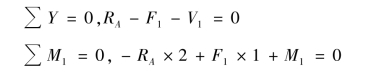
解得:

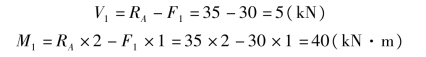
求得V1 和M1 均为正值,表示1—1 截面上内力的实际方向与假定的方向相同;按内力的符号规定,剪力、弯矩都是正的。所以,画受力图时一定要先假设内力为正的方向,由平衡方程求得结果的正负号,就能直接代表内力本身的正负。

如取1—1 截面右段梁为研究对象[图9.9(c)],可得出同样的结果。

【例9.2】　一悬臂梁的尺寸及梁上荷载如图9.10 所示,求1—1 截面上的剪力和弯矩。

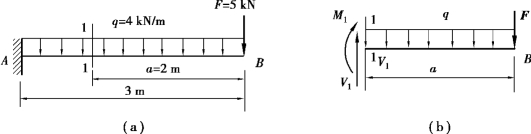
图9.10

【解】　对于悬臂梁,可取右段梁为研究对象,不需求支座反力,其受力图如图9.10(b)所示。

解得:

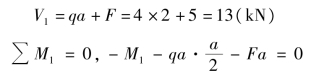
解得:

求得V1 为正值,表示V1 的实际方向与假定的方向相同;M1 为负值,表示M1 的实际方向与假定的方向相反。所以,按梁内力的符号规定,1—1 截面上的剪力为正,弯矩为负。