圆轴扭转时的内力：探究扭矩

在对圆轴进行强度计算之前,先要计算出圆轴横截面上的内力——扭矩。

1)扭矩

如图7.10(a)所示圆铀,在垂直于轴线的两个平面内,受一对外力偶矩Me 作用,现求任一截面m—m 的内力。

求内力的基本方法仍是截面法,用一个假想横截面在轴的任意位置m—m 处将轴截开,取左段为研究对象,如图7.10(b)所示。由于左端受一个外力偶Me 作用,为了保持左段轴的平衡,左截面m—m 的平面内,必然存在一个与外力偶相平衡的内力偶,其内力偶矩Mn 称为扭矩,大小由∑Mx = 0,得:

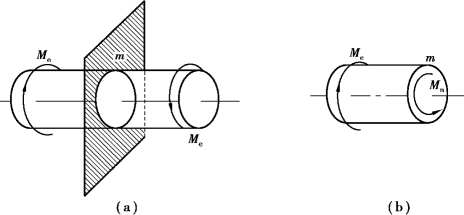
图7.10

如取m—m 截面右段轴为研究对象,也可得到同样的结果,但转向相反。

扭矩的单位与力矩相同,常用N·m 或kN·m。

2)扭矩正负号规定

为了使由截面的左、右两段轴求得的扭矩具有相同的正负号,对扭矩的正、负做如下规定:采用右手螺旋法则,以右手四指表示扭矩的转向,当拇指的指向与截面外法线方向一致时,扭矩为正;反之为负,如图7.11 所示。

图7.11

除轴的两端外,如果轴的其他位置还有外力偶矩作用,则轴上每一段的扭矩值将不尽相同,这时轴的扭矩应分段计算。与拉伸(压缩)问题中绘制轴力图相仿,可用图线来表示各横截面上扭矩沿轴线的变化情况。表示扭矩沿杆轴线的变化规律的图线,称为扭矩图。

作用在轴上的外力偶矩,一般可根据已知的外载荷由静力平衡方程确定。然而,工程中的传动轴,往往只给出轴所传递的功率和轴的转速。这时,需通过计算来确定外力偶矩。(www.xing528.com)

若已知传动轴的转速为n(单位:r/min,转/分),所传递的功率为N(单位:kW,千瓦),则可得外力偶矩m 的计算公式为:

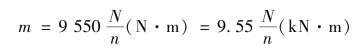
【例7.3】　如图7.12(a)所示,圆轴直径为d=40 mm,轴上装有3 个皮带轮,已知由轮3 输入的功率N3 =30 kW,轮2 的输出功率N2 =17 kW,轮1 的输出功率N1 =13 kW,轴的转速n =200 r/min,试绘扭矩图。

【解】　①计算外力偶矩。

图7.12

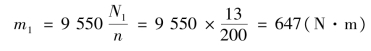
②用截面法计算各段的扭矩。扭矩按正方向假设,从受载荷情况知道,轴AB、BC 两段内各截面上的扭矩不相等。在AB 段内,假设用Mn1表示截面1—1 上的扭矩,如图7.12(b)所示,由平衡方程可得:

同理,在BC 段,如图7.12(c)所示,由平衡方程得:

计算结果Mn1及Mn2为负值,表示假设的转向与实际扭向相反。

③作出扭矩图,如图7.12(d)所示。从图7.12(d)中看出,最大扭矩发生于BC 段。