对于工程上常用的材料,如低碳钢、合金钢等所制成的轴向拉(压)杆,有实验证明:当杆的应力未超过某一极限时,纵向变形Δl 与外力P、杆长l 及横截面面积A 之间存在如下比例关系:
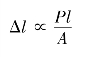
引入比例常数E,则有:
![]()
实际上引起伸长的是内力N,当杆只在两端受力P 时,杆段轴力N=P。当杆段轴力不等于P 时,可将上式改写成:

这一比例关系,是1678年首先由英国科学家胡克提出的,故称为胡克定律。式中比例常数量称为弹性模量,从式(6.4)知,当其他条件相同时,材料的弹性模量越大,则变形越小,它表示材料抵抗弹性变形的能力。E 的数值随材料而异,是通过实验测定的,其单位与应力单位相同。EA 称为杆件的抗拉(压)刚度。对于长度相等且受力相同的拉杆,其抗拉(压)刚度越大,则变形就越小。
将式(6.1)及式(6.2)代入式(6.4)可得:
![]()
式(6.5)是胡克定律的另一表达形式,它表明当杆件应力不超过某一极限时,应力与应变成正比。
上述的应力极限值,称为材料的比例极限,用σp 表示(详见下一节)。![]() 故α=57.53°,sin α=0.843,cos α=0.537。代入式(1)、(2)解得:
故α=57.53°,sin α=0.843,cos α=0.537。代入式(1)、(2)解得:
【例6.5】 为了测定钢材的弹性模量E 值,将钢材加工成直径d =10 mm 的试件,放在实验机上拉伸。当拉力P 达到15 kN 时,测得纵向线应变ε=0.000 96,求钢材的弹性模量。
【解】 当P 达到15 kN 时,正应力为:
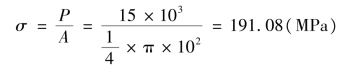
由胡克定律σ=E·ε 得:
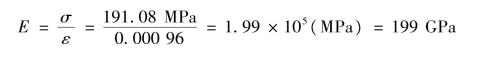 (https://www.xing528.com)
(https://www.xing528.com)
【例6.6】 图6.10 所示为一方形截面砖柱,上段柱边长为240 mm,下段柱边长370 mm。荷载F=40 kN,不计自重,材料的弹性模量E=0.03 ×105 MPa,试求砖柱顶面A 的位移。
【解】 绘出砖柱的轴力图,如图6.10(b)所示。设砖柱顶面A 下降的位移为Δl,显然它的位移就等于全柱的总缩短量,由于上、下两段柱的截面面积及轴力都不相等,故应分别求出两段柱的变形,然后求其总和。
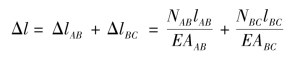
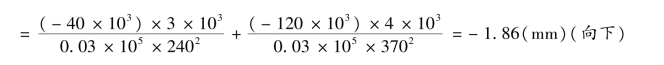
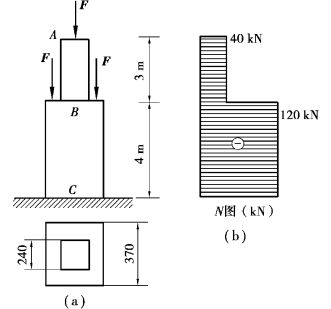
图6.10
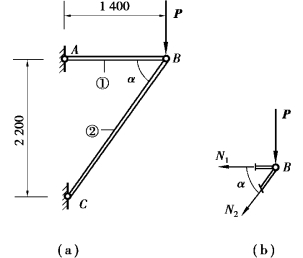
图6.11
【例6.7】 计算图6.11(a)所示结构杆①及杆②的变形,已知杆①为钢杆,A1 =8 cm2,E1 =200 GPa;杆②为木杆,A2 =400 cm2,E2 =12 GPa,P=120 kN。
【解】 ①求各杆的轴力。取B 结点为研究对象[图6.11(b)],列平衡方程得:

因
![]()
②计算杆的变形。
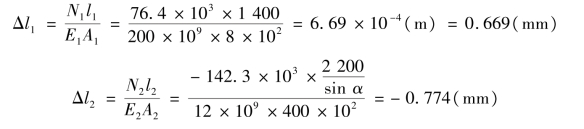
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




