要解决轴向拉压杆是否破坏的强度问题,不但要知道杆件的内力,还必须知道内力在截面上的分布规律。应力在横截面上的分布不能直接观察到,但内力与变形有关。因此,要找出内力在截面上的分布规律,通常采用的方法是先做实验。根据由实验观察到的杆件在外力作用下的变形现象,做出一些假设,然后才能推导出应力计算公式。下面采用这种方法推导轴向拉压杆的应力计算公式。
取一根等直杆[图6.6(a)],为了便于通过实验观察轴向受拉杆所发生的变形现象,受力前在杆件表面均匀地画上若干与杆轴线平行的纵线及与轴线垂直的横线,使杆表面形成许多大小相同的方格。然后在杆的两端施加一对轴向拉力P[图6.6(b)],可以观察到,所有的纵线仍保持为直线,各纵线都伸长了,但仍互相平行,小方格变成长方格。所有的横线仍保持为直线,且仍垂直于杆轴,只是相对距离增大了。

图6.6
根据上述现象,可作如下假设:
①平面假设。若将各条横线看作一个横截面,则杆件横截面在变形以后仍为平面且与杆轴线垂直,任意两个横截面只是做相对平移。
②若将各纵向线看作是杆件由许多纤维组成,根据平面假设,任意两横截面之间的所有纤维的伸长都相同,即杆件横截面上各点处的变形都相同。
由于前面已假设材料是均匀连续的,而杆件的分布内力集度又与杆件的变形程度有关,因此从上述均匀变形的推理可知,轴向拉杆横截面上的内力是均匀分布的,也就是横截面上各点的应力相等。由于拉压杆的轴力垂直于横截面,故与它相应的分布内力也必然垂直于横截面。由此可知,轴向拉杆横截面上只有正应力,而没有剪应力。据此可得结论:轴向拉伸时,杆件横截面上各点处只产生正应力,且大小相等[图6.6(c)]。

式中 N——杆件横截面上的轴力;
A——杆件的横截面面积。
当杆件受轴向压缩时,上式同样适用。由于前面已规定了轴力的正负号,由式(6.1)可知,正应力也随轴力N 而有正负之分,即拉应力为正,压应力为负。![]()

图6.7
【例6.3】 如图6.7(a)所示的等直杆,当截面为50 mm×50 mm 正方形时,试求杆中各段横截面上的应力。
【解】 计算杆的横截面面积。(https://www.xing528.com)
![]()
绘出杆的轴力图如图6.7(b)所示。由正应力计算公式可得:
①AB 段内任一横截面上的应力:
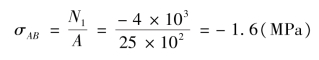
②BC 段内任一横截面上的应力:

【例6.4】 图6.8(a)所示为铆钉连接主板的受力图。已知板宽b=160 mm,板厚c=10 mm,钉孔直径d=20 mm,荷载F=160 kN。铆钉对钉孔的作用用集中力F1 表示,求主板的最大正应力。
【解】 ①轴力图。坐标轴略去不画,以基线代替x 轴。在集中力作用点处分区段,逐段作图[图6.8(b)]。
②最大正应力计算。由横截面正应力公式σ =N/A 分析,在N 相等的各个截面中,净面积A 小的横截面的正应力大。图6.8(b)所示轴力相等的杆段中,过钉孔圆心的横截面的净面积最小,可见杆的σmax只能发生在1—1、2—2 或3—3 截面[图6.8(a)];在面积相等的横截面中,轴力大的截面正应力大,可见1—1 截面的正应力比3—3 截面的正应力大。杆的σmax只能发生在1—1 或2—2 截面;对于N 大、A 也大和N 小、A 也小的截面,须计算正应力比较其大小[图6.8(c)]。
1—1 截面:

2—2 截面:


图6.8
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




