平面一般力系的平衡方程应用技巧

现举例说明,应用平面一般力系的平衡条件,来求解工程实际中物体平衡问题的步骤和方法。

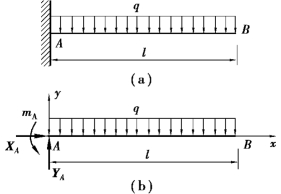
图4.12

【例4.3】　悬臂梁AB 受荷载作用,如图4.12(a)所示。一端为固定端支座约束,另一端为自由端的梁,称为悬臂梁。已知线分布荷载q =2 kN/m,l =2 m,梁的自重不计。求固定端支座A 处的约束反力。

【解】　取梁AB 为研究对象,受力分析如图4.12(b)所示。支座反力的指向均为假设,梁上所受的荷载与支座反力组成平面一般力系。

梁上的均布荷载可先合成为合力Q,其大小Q =ql,方向铅垂向下,作用在AB 梁的中点。选取坐标系如图4.12(b)所示,列一矩式的平衡方程如下:

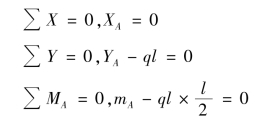
解得:

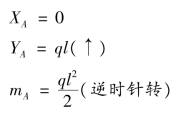
求得结果为正值,说明假设约束反力的指向与实际相同。

校核:

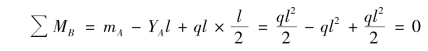
可见,YA和mA计算无误。

由此例可以得出结论:对于悬臂梁和悬臂刚架,均适合于采用一矩式平衡方程求解支座反力。

【例4.4】　简支刚架如图4.13(a)所示。已知P =15 kN,m=6 kN·m,Q=20 kN,求A、B处的支座反力。

【解】　取刚架整体为研究对象,受力分析如图4.13(b)所示,支座反力的指向均为假设,刚架上所受的荷载与支座反力组成平面一般力系。选取坐标系如图4.13(b)所示,列二矩式的平衡方程如下:

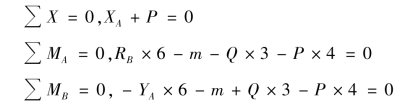
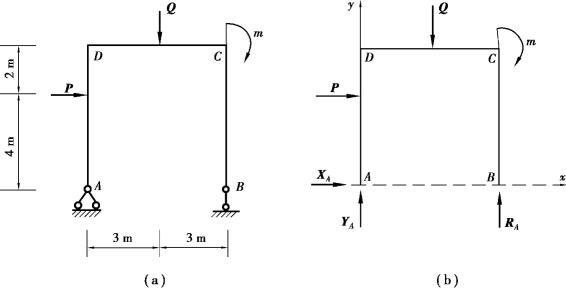
图4.13

解得:

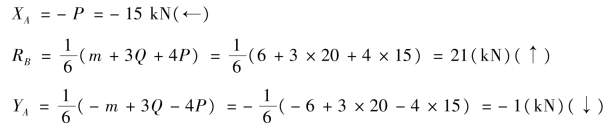
求得结果XA、YA为负值,说明假设的指向与实际相反;RB为正值,说明假设约束反力的指向与实际相同。

校核:

说明计算无误。

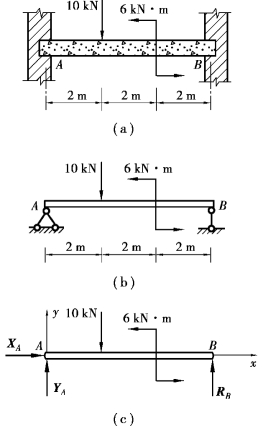
图4.14

由此例可得出结论:对于简支梁、简支刚架,均适合于采用二矩式平衡方程求解支座反力。

【例4.5】　某房屋中的梁AB 两端支承在墙内,构造及尺寸如图4. 14(a)所示。该梁简化为简支梁,如图4.14(b)所示,不计梁的自重。求墙壁对梁A、B 端的约束反力。

【解】　①取简支梁AB 为研究对象。

②受力分析如图4.14(c)所示。约束反力XA、YA 和RB 的指向均为假设,梁受平面一般力系的作用。

③取如图4.14(c)所示坐标系,列二矩式的平衡方程如下:

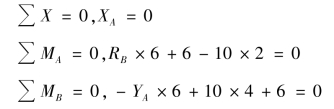
④求解未知量。

⑤校核。

说明计算无误。

【例4.6】　悬臂式起重机尺寸及受荷载如图4.15(a)所示,A、B、C 处都是铰链连接。已知梁AB 自重G=6 kN,匀速提升重量P=15 kN。求铰链A 的约束反力及拉杆BC 所受的力。

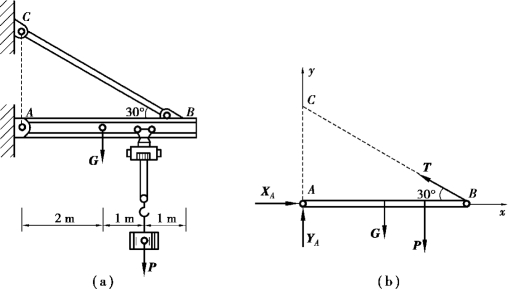
图4.15

【解】　①选取梁AB 为研究对象。

②受力分析如图4.15(b)所示。在梁上受已知力P 和G 作用。求未知力:二力杆BC 的拉力T、铰链A 的约束反力XA 和YA。这些力的作用线在同一平面内组成平面一般力系。

③列平衡方程。由于梁AB 处于平衡状态,因此力系满足平面一般力系的平衡条件。取坐标轴如图4.15(b)所示,列三矩式的平衡方程如下:

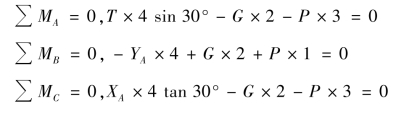(www.xing528.com)

④求解未知量。

求出结果均为正值,说明假设反力的指向与实际方向相同。

⑤校核。

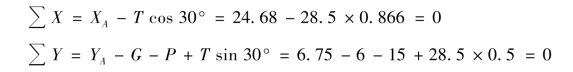
计算无误。

由此例可得出结论:对于三角支架,适合于采用三矩式平衡方程求解约束反力。

从上述例题可见,选取适当的坐标轴和矩心,可以减少每个平衡方程中的未知量的数目。在平面一般力系情况下,力矩应取在两未知力的交点上,而投影轴尽量与多个未知力垂直。

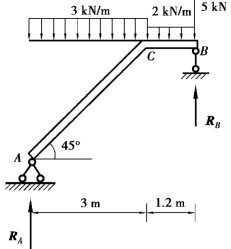
图4.16

【例4.7】　如图4.16 所示,均布荷载沿水平方向分布,求此梁支座A 和B 处的支反力。

【解】　取整体ABC 为研究对象。受力分析如图4.16 所示,则此梁受平面平行力系作用,列出二矩式的平衡方程如下:

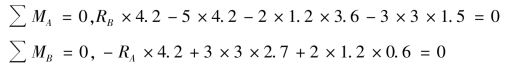
解得:

校核:

计算无误。

【例4.8】　某房屋的外伸梁构造及尺寸如图4.17(a)所示。该梁的力学简图如图4.17(b)所示。已知q1 =20 kN/m,q2 =25 kN/m。求A、B 支座的反力。

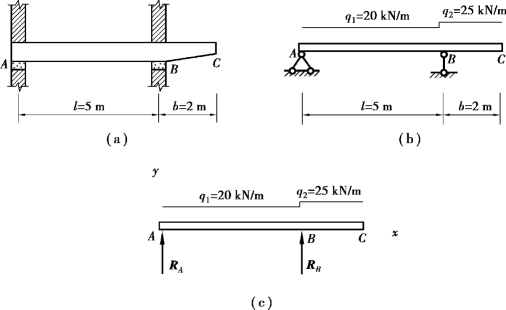
图4.17

【解】　①取外伸梁AC 为研究对象。

②受力分析如图4.17(c)所示。约束反力RA 和RB 假设向上,梁受平面平行力系的作用。

③取如图4.17(c)所示坐标系,列二矩式的平衡方程如下:

④求解未知量。

⑤校核。

说明计算无误。

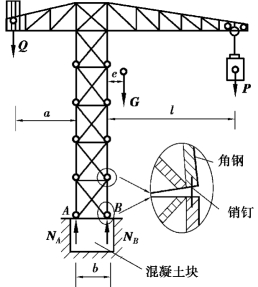
图4.18

【例4.9】　图4.18 所示为塔式起重机。已知b =2 m,机身重G=240 kN,其作用线到右侧的距离e=1.5 m,起重机的平衡块重为Q,其作用线到左侧的距离a =6 m,荷载P 的作用线到右侧的距离l=12 m。试确定:起重机的平衡块的重量Q 的大小值;起重机不向右倾倒的最大起重荷载P 为多少?

【解】　取起重机为研究对象。受力分析如图4.18所示,作用于起重机上的主动力有G、P、Q,约束反力有NA 和NB,NA 和NB 均铅垂向上,以上各力组成平面平行力系。

②确定平衡块重量Q。A、B 支座是用螺栓与混凝土墩相连的,受拉时主要靠螺母上的丝来承受拉力,故能承受的拉力很小,偏安全地以A、B 支座不承受拉力来确定平衡块的重量计算。空载P =0 时,平衡块重量Q 引起的右侧铰受拉力最大,要右铰不受拉,只需满足条件NB≥0。以A 点为矩心,列平衡方程:

解得:

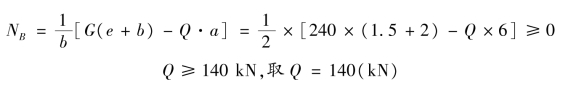
③使起重机不向右倾倒的条件是左边铰不受拉,即NA≥0。以B 点为矩心,列平衡方程:

解得:

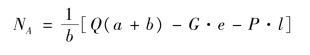
要使NA≥0,则需:

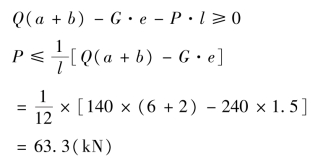
当荷载P≤63.3 kN 时,起重机不会向右倾倒。