平面一般力系的平衡条件

平面一般力系向平面内任一点简化,若主矢R′和主矩MO 同时等于零,表明作用于简化中心O 点的平面汇交力系和附加平面力偶系都自成平衡,则原力系一定是平衡力系;反之,如果主矢R′和主矩MO 中有一个不等于零或两个都不等于零时,则平面一般力系就可以简化为一个合力或一个力偶,原力系就不能平衡。因此,平面一般力系平衡的必要与充分条件是力系的主矢和力系对平面内任一点的主矩都等于零。

1)平衡方程的基本形式

由于

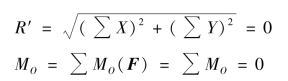
于是,平面一般力系的平衡条件为:

式中∑MO(F) 也可简写成∑MO,以下相同。

由此得出结论,平面一般力系平衡的必要与充分的解析条件是:力系中所有各力在任意选取的两个坐标轴中的每一轴上投影的代数和分别等于零;力系中所有各力对平面内任意点之矩的代数和也等于零。式中包含两个投影方程和一个力矩方程,是平面一般力系平衡方程的基本形式。这3 个方程是彼此独立的,可求出3 个未知量。

2)平衡方程的其他形式

前面通过平面一般力系的平衡条件导出了平面一般力系平衡方程的基本形式,除此之外,还可以将平衡方程改写成二矩式和三矩式的形式。

(1)二力矩式

3 个平衡方程中有一个为投影方程,两个为力矩方程。(www.xing528.com)

式中,x 轴不能与A、B 两点的连线垂直。

可以证明:式(4.6) 也是平面一般力系的平衡方程。因为,如果力系对点A 的主矩等于零,则这个力系不可能简化为一个力偶,但可能有两种情况:这个力系或者是简化为经过点A 的一个力R,或者平衡;如果力系对另外一点B 的主矩也同时为零,则这个力系或简化为一个沿A、B两点连线的合力R,或者平衡;如果再满足∑X = 0,且x 轴不与A、B 两点连线垂直,则力系也不能合成为一个合力,若有合力,合力在x 轴上就必然有投影。因此,力系必然平衡。

(2)三力矩式

3 个平衡方程都为力矩方程。

式中,A、B、C 3 点不共线。

同样可以证明,式(4.7)也是平面一般力系的平衡方程。因为,如果力系对A、B 两点的主矩同时等于零,则力系或者是简化为经过点A、B 两点的一个力R,或者平衡;如果力系对另外一个C 点的主矩也同时为零,且C 点不在A、B 两点的连线上,则力系就不可能合成为一个力,因为一个力不可能同时通过不在一直线上的三点(图4.9、图4.10)。因此,力系必然平衡。

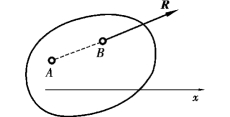
图4.9

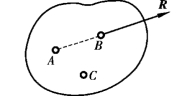
图4.10

上述3 组方程都可以用来解决平面一般力系的平衡问题。究竟选取哪一组方程,需根据具体条件确定。对于受平面一般力系作用的单个物体的平衡问题,只可以写出3 个独立的平衡方程,求解3 个求知量。任何第四个方程都是不独立的,可以利用不独立的方程来校核计算结果。