平面一般力系的合力矩定理优化：如何计算平面力系的合力矩？

由上面分析可知,当R′≠0,MO≠0 时,还可进一步简化为一个合力R,如图4.6 所示。合力对O 点的矩为:

而

所以

由于简化中心O 点是任意选取的,故上式有普遍的意义。于是可得到平面力系的合力矩定理。平面一般力系的合力对其作用面内任一点之矩等于力系中各力对同一点之矩的代数和。

【例4.1】　如图4.7(a)所示,梁AB 的A 端是固定端支座,试用力系向某点简化的方法说明固定端支座的反力情况。

【解】　梁的A 端嵌入墙内成为固定端,固定端约束的特点是使梁的端部既不能移动也不能转动。在主动力作用下,梁插入部分与墙接触的各点都受到大小和方向都不同的约束反力作用[图2.17(b)]。这些约束反力就构成一个平面一般力系,将该力系向梁上A 点简化就得到一个力RA 和一个力偶矩为MA 的力偶。为了便于计算,一般可将约束反力RA 用它的水平分力XA和竖直分力YA 来代替。因此,在平面力系情况下,固定端支座的约束反力包括3 个:即阻止梁端向任何方向移动的水平反力XA 和竖向反力YA,以及阻止物体转动的反力偶MA。它们的指向都是假定的。

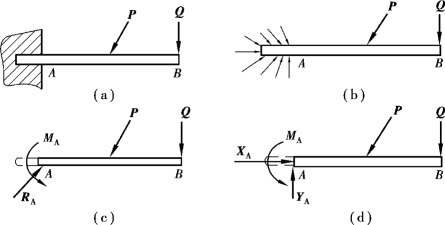
图4.7

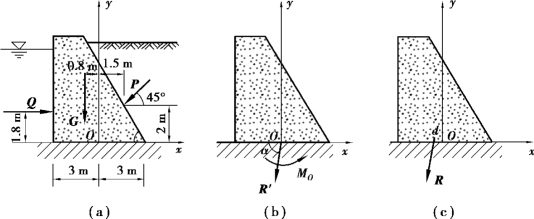
【例4.2】　挡土墙受力情况如图4.8 所示。已知自重G=420 kN,土压力P=300 kN,水压力Q=180 kN。试将这3 个力向底面中心O 点简化,并求最后的简化结果。

(www.xing528.com)

图4.8

【解】　①先将力系向O 点简化,取坐标系如图4.8(b)所示。由式可求得主矢R′的大小和方向。由于

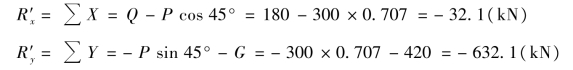
所以

因为∑X 和∑Y 都是负值,故R′指向为第三象限,与x 轴的夹角为α。

再由式(4.4)可求得主矩:

计算结果为正值,表示主矩MO 是逆时针转向。

因挡土墙处于平衡状态,故地基反力与R′和MO 相反,可将其分解为水平反力XO 和竖向反力YO,以及阻止物体转动的反力偶MO。

②求最后的简化结果。因为主矢R′≠0, 主矩MO≠0,如图4.8(b)所示,所以还可以进一步合成为一个合力R。R 的大小和方向与R′相同,它的作用线与O 点距离为:

因MO(R)也为正,即合力R 应在O 点左侧,如图4.8(c)所示。